证明复杂性

在逻辑学和理论计算机科学中，特别是证明理论和计算复杂性理论，证明复杂性是一个旨在理解和分析证明或反驳语句所需的计算资源的领域。证明复杂性的研究主要是在各种命题证明系统中证明长度的下限和上限。例如，证明复杂性的主要挑战之一是表明弗雷格系统，即通常的命题微积分，不允许对所有同义词进行多项式证明。在这里，证明的大小只是其中的符号数，如果一个证明是它所证明的同义反复的大小，那么它就被称为多项式大小。对证明复杂性的系统研究始于StephenCook和RobertReckhow（1979）的工作，他们从计算复杂性的角度提供了命题证明系统的基本定义。具体来说，Cook和Reckhow观察到，在越来越强的命题证明系统上证明大小的下限可以被看作是将NP与coNP（从而将P与NP）分开的一个步骤，因为存在一个对所有同义词都承认多项式大小证明的命题证明系统，就等同于NP=coNP。当代证明复杂性研究从计算复杂性、算法和数学的许多领域中汲取了思想和方法。由于许多重要的算法和算法技术可以作为某些证明系统的证明搜索算法，证明这些系统中证明大小的下限意味着相应算法的运行时间下限。这就把证明复杂性与更多的应用领域联系起来，如SAT求解。数理逻辑也可以作为一个框架来研究命题证明大小。一阶理论，特别是Peano算术的弱片段，在有界算术的名义下，作为命题证明系统的统一版本，并提供进一步的背景，以不同层次的可行推理来解释短命题证明。

一个命题证明系统被给出为一个有两个输入的证明验证算法P(A,x)。如果P接受一对(A,x)，我们就说x是A的一个P证明。P被要求在多项式时间内运行，此外，当且仅当A是一个同义词时，它必须保持A有一个P证明。命题证明系统的例子包括顺序计算、解析、切割平面和弗雷格系统。诸如ZFC这样的强数学理论也会引起命题证明系统：一个同义词的证明{displaystyletau}是一个同义反复。是一个同义词'。多项式大小的证明和NP与coNP的问题证明复杂性通常以系统中对给定同义词可能的最小证明大小来衡量证明系统的效率。

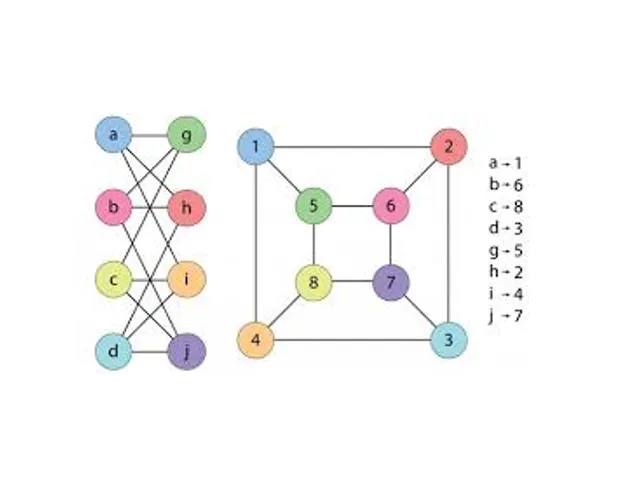
一个证明（分别是公式）的大小是表示该证明（分别是公式）所需的符号数。如果存在一个常数，那么一个命题证明系统P是多项式有界的.证明复杂性的一个核心问题是了解同义词是否承认多项式大小的证明。从形式上看。问题（NPvs.coNP）是否存在一个多项式约束的命题证明系统？Cook和Reckhow(1979)指出，当且仅当NP=coNP时，存在一个多项式约束的证明系统。因此，证明特定的证明系统不承认多项式大小的证明，可以看作是分离NP和coNP（从而分离P和NP）的一个部分进展。

证明复杂性使用模拟的概念对证明系统的强度进行比较。如果存在一个多项式时间函数，给定一个同义词的Q证明，就能输出同一同义词的P证明，则证明系统P就能模拟一个证明系统Q。如果P模仿Q，Q模仿P，则证明系统P和Q是p等价的。还有一个更弱的模拟概念：如果存在一个多项式p，使得对于同义词A的每一个Q-证明x，都有一个A的P-证明y，使得y的长度|y|最多为p(|x|)，则证明系统P模拟证明系统Q。例如，序列微积分与（每个）弗雷格系统是p等价的。如果一个证明系统p模拟所有其他的证明系统，那么它就是p最优的，如果它模拟所有其他的证明系统，那么它就是最优的。这样的证明系统是否存在，是一个开放性问题。问题(最优性)是否存在一个p-最优或最佳的命题证明系统？每一个命题证明系统P都可以通过扩展的弗雷格（ExtendedFrege）来模拟，扩展的公理规定了P的合理性。