下采样（信号处理）

在数字信号处理中，下采样、压缩和抽取是与多速率数字信号处理系统中重采样过程相关的术语。

下采样和去分化都可以是压缩的同义词，或者它们可以描述带宽减少（过滤）和采样率降低的整个过程。当这个过程在一个信号或连续函数的样本序列上进行时，它产生了一个以较低速率（或密度，如照片）对信号进行采样所得到的序列的近似值。

十边形是一个术语，在历史上意味着去除每十个一。但在信号处理中，十进位的系数实际上意味着只保留每十个样本。这个系数乘以采样间隔，或者说，等同于除以采样率。

例如，如果44,100样本/秒的光盘音频被抽取5/4的系数，那么得到的采样率是35,280。一个执行抽取的系统组件被称为抽取器。以一个整数系数进行的抽取也被称为压缩。

按整数因子M降低采样率可以解释为一个两步的过程，有一个等效的实现方法，效率更高。用数字低通滤波器减少高频信号成分。将过滤后的信号按M分解；也就是说，只保留每第M个样本。仅仅是步骤2就会使高频信号成分被数据的后续使用者误解，这是一种称为混叠的失真。必要时，步骤1可以将混叠抑制到一个可接受的水平。

在这种应用中，该滤波器被称为抗混叠滤波器，其设计将在下面讨论。关于带通函数和信号的抽取，也请看低取样的信息。当抗混叠滤波器是一个IIR设计时，它依赖于在第二步之前从输出到输入的反馈。有了FIR滤波，只计算每第M个输出是一件很容易的事。一个去噪的FIR滤波器对第n个输出样本进行的计算是一个点积。其中h[-]序列是脉冲响应，K是其长度。在通用处理器中，在计算完y[n]后，计算y[n+1]的最简单方法是将x[-]阵列中的起始索引提前M，然后重新计算点乘。在M=2的情况下，h[-]可以被设计成一个半带滤波器，其中几乎一半的系数是零，不需要包括在点乘中。以M的间隔取的脉冲响应系数构成一个子序列，有M个这样的子序列（相位）被复用在一起。

点积是每个子序列与x[-]序列的相应样本的点积之和。此外，由于M的下采样，M个点积中的任何一个所涉及的x[-]样本流都不会涉及其他的点积。

因此，M个低阶FIR滤波器分别对输入流的M个复用阶段中的一个进行过滤，而M个输出则被相加。这种观点提供了一种不同的实现方式，在多处理器结构中可能是有利的。

换句话说，输入流被解复用，并通过一个由M个滤波器组成的银行，其输出被相加。当以这种方式实现时，它被称为多相滤波器。

为了完整起见，我们现在提到一个可能的，但不太可能的，每个阶段的实现方式是在h[-]阵列的副本中用0替换其他阶段的系数，以输入速率处理原始x[-]序列（这意味着乘以0），并将输出降低M的因子。

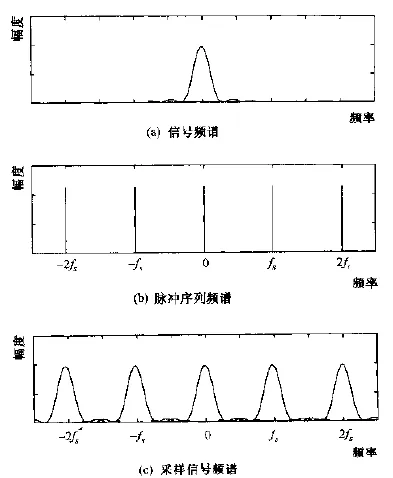
它有时被用于多相法的推导中。抗混叠滤波器让X(f)是任何函数x(t)的傅里叶变换，其在某个区间T的样本等于x[n]序列。

那么离散时间傅里叶变换（DTFT）是X(f)的周期性求和的傅里叶序列表示。有赫兹的单位。