有限体积法
编辑命名微分方程的清单分类类型与过程的关系微分(离散类似物)随机性随机性部分延迟解存在性和唯一性
检验法
编辑在中,包含发散项的偏微分方程中的体积积分被转换为表面积分,使用发散定理。然后这些项被评估为每个有限体积表面的通量。因为进入一个给定体积的通量与离开相邻体积的通量是相同的,所以这些方法是保守的。
有限体积法的另一个优点是,它很容易被制定为允许非结构化网格的方法。有限体积法在许多计算流体力学软件包中都有应用。有限体积指的是网格上每个节点点周围的小体积。有限体积法可以与有限差分法和有限元法进行比较,前者使用节点值对导数进行近似,后者使用局部数据对解进行局部近似,并通过拼接构建全局近似。与此相反,有限体积法评估了一些体积上的解决方案的平均值的精确表达式,并使用这些数据来构建单元内的解决方案的近似值。
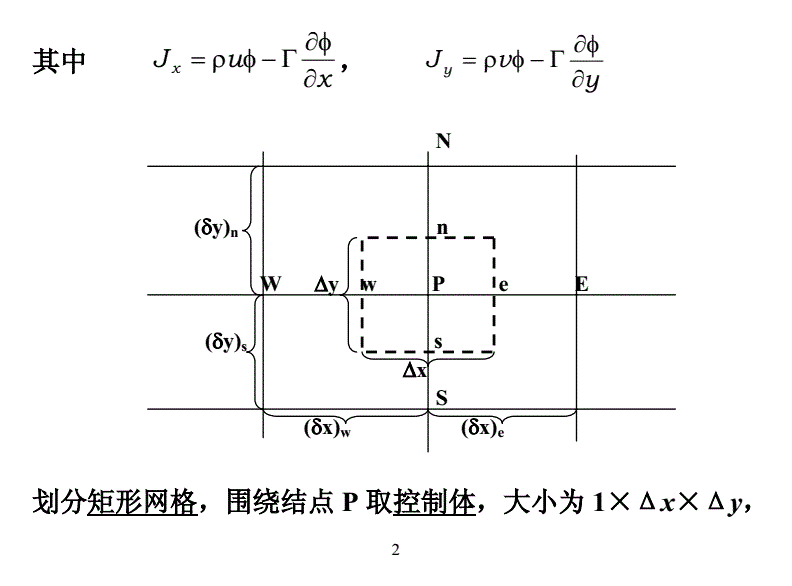
有限体积法的例子
编辑考虑一个简单的一维平流问题。代表向左的流动。如果我们假设方程(1)代表一个面积不变的流动介质,我们可以对空间域进行细分。划分为有限体积或单元,并将这些单元分为两个部分。分为有限体积或单元,并且我们认为是行为良好的,并且我们可以扭转积分的顺序。另外,回顾一下,流动是对单元的单位面积的法线。我们可以应用发散定理,我们可以应用发散定理。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/168376/
