线性逼近
编辑在数学中,线性逼近是使用线性函数(更确切地说,是仿生函数)对一般函数进行的逼近。它们被广泛用于有限差分法中,以产生解决或逼近方程解的一阶方法。
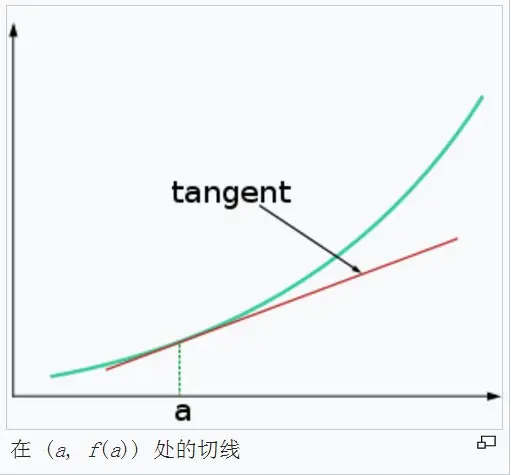
线性逼近的定义
编辑给定一个两次连续可微的函数时,这是一个很好的近似值。;因为当仔细观察时,曲线会开始类似于直线。因此,右手边的表达式只是一个切线的方程,近似值将是一个高估(因为导数在该区间是递减的)。如果f是向上凹陷的,那么近似值将是一个低估。是向上凹陷的,近似值将是一个低估。矢量变量的矢量函数的线性近似也是以同样的方式得到的,在某一点的导数由雅各布矩阵代替。例如,给定一个可微的函数
线性逼近的应用
编辑线性逼近的光学
编辑高斯光学是几何光学中的一种技术,它通过使用准轴近似来描述光学系统中光线的行为,其中只考虑与系统的光轴成小角的光线。在这种近似中,三角函数可以被表达为角度的线性函数。高斯光学适用于所有的光学表面都是平的或者是球体的一部分的系统。在这种情况下,可以根据组成元素的几何形状和材料特性,为成像系统的参数,如焦距、放大率和亮度,给出简单明确的公式。
摆动周期
编辑一个简单的重力摆的摆动周期取决于它的长度,当地的重力强度,以及在很小的程度上取决于摆锤离开垂直方向的最大角度,θ0,称为振幅。它与小棒的质量无关。简单摆的真实周期T,即一个理想的简单重力摆一个完整周期所需的时间,可以写成几种不同的形式(见摆),一个例子是无限级数。其中L是摆的长度,g是当地的重力加速度。然而,如果采取线性近似法(即如果振幅仅限于小幅摆动,),则周期为。(1)在线性近似中,不同大小的摆动的周期是大致相同的:也就是说,周期与振幅无关。这一特性,称为等时性,是钟摆在计时方面如此有用的原因。摆的连续摆动,即使在振幅上有变化,也需要相同的时间。
电阻率
编辑大多数材料的电阻率随温度变化。如果温度T没有变化太大,通常使用线性近似法。被称为电阻率的温度系数。被称为电阻率的温度系数。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/168434/
