同态滤波

同态滤波是一种用于信号和图像处理的通用技术，涉及到一个非线性映射到不同的领域，在这个领域中应用线性滤波技术，然后再映射回原领域。这一概念是由麻省理工学院的ThomasStockham、AlanV.Oppenheim和RonaldW.Schafer在20世纪60年代提出的，并由Bogert、Healy和Tukey在研究时间序列时独立提出。

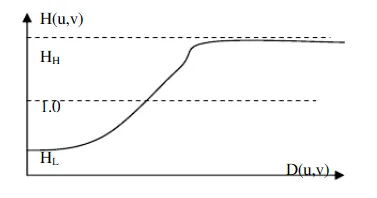
同态过滤有时被用于图像增强。它同时使整个图像的亮度正常化并增加对比度。在这里，同态滤波被用来去除乘法噪声。照度和反射率是不可分离的，但它们在频域中的近似位置可以被定位。由于照度和反射率是乘法结合的，通过对图像强度取对数，使这些成分成为加法，因此图像的这些乘法成分可以在频域中线性地分离。光照变化可以被认为是一种乘法噪声，可以通过在对数域的过滤来减少。为了使图像的照度更加均匀，高频分量被增加，低频分量被减少，因为高频分量被认为主要代表场景中的反射率（场景中物体反射的光量），而低频分量被认为主要代表场景中的照度。也就是说，在对数强度域中，高通滤波是用来抑制低频和放大高频的。操作同态滤波可用于改善灰度图像的外观，同时进行强度范围压缩（照明）和对比度增强（反射）。我们必须将该方程转换为频域，以便应用高通滤波器。然而，在对这个方程进行傅里叶变换后，要进行计算是非常困难的，因为它不再是一个乘积方程。因此，我们使用"log"来帮助解决这个问题。接下来，对图像应用高通滤波器。为了使图像的照度更加均匀，高频成分被增加，低频成分被减少。N(u,v)=H(u,v)∙M(u,v){displaystyleN(u,v)=H(u,v)/bulletM(u,v)}。其中H=任何高通滤波器N=频域中过滤后的图像之后，通过使用反傅里叶变换将频域返回到空间域。

下面的数字显示了应用同态滤波器、高通滤波器和同态与高通滤波器的结果。所有的数字都是用Matlab制作的。根据图一到图四，我们可以看到同态滤波是如何用于纠正图像中的非均匀光照的，并且图像变得比原始图像更清晰。另一方面，如果我们对同态滤波的图像应用高通滤波器，图像的边缘会变得更清晰，而其他区域会变得更暗淡。这个结果与只对原始图像进行高通滤波相似。

有人认为，许多相机已经有一个近似对数的响应函数（或更普遍的，一个倾向于压缩动态范围的响应函数），而显示媒体，如电视显示器，摄影印刷媒体等，有一个近似反对数的响应，或一个其他动态范围扩张的响应。因此，只要我们在真正的光量单位q上处理像素值f(q)，同态滤波就会意外地（无意地）发生。因此有人提出，另一种有用的滤波是反同态滤波，其中图像f(q)首先被动态范围扩展以恢复真正的光量q，在此基础上进行线性滤波，然后再将动态范围压缩到图像空间，以便显示。

同态滤波是在对数频谱域中使用的，以将滤波效果与激励分开。