模糊数学

模糊数学是数学的一个分支，包括模糊集合理论和模糊逻辑，它处理一个集合中的元素在频谱上的部分包含，而不是简单的二进制是或否（0或1）包含。语言学是一个利用模糊集理论的领域的例子。

一个集合X的模糊子集A是一个函数A：X→L，其中L是区间[0，1]。这个函数也被称为成员函数。成员函数是对L={0，1}定义的子集的指标函数（也叫特征函数）的泛化。更一般地说，人们可以在模糊子集A的定义中使用任何完整的网格L。

数学概念的模糊化的演变可以分为三个阶段。通常，数学概念的模糊化是基于这些概念从特征函数到成员函数的泛化。设A和B是X的两个模糊子集，交集A∩B和并集A∪B定义如下。(A∩B)(x)=min(A(x),B(x)),(A∪B)(x)=max(A(x),B(x))对于X中的所有x，人们可以分别使用t-norm和t-conorm代替min和max；例如，min(a,b)可以用乘法ab代替。一个直接的模糊化通常是基于最小和xxx的操作，因为在这种情况下，传统数学的更多属性可以扩展到模糊的情况。代数运算的模糊化中使用的一个重要的概括原则是封闭属性。让*是X上的一个二元运算。

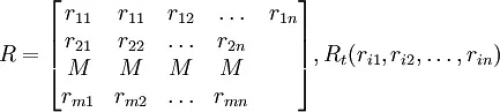
X的模糊子集A的封闭属性是：对于X中的所有x，y，A(x*y)≥min(A(x),A(y))。假设(G,*)是一个群，A是G的一个模糊子集，那么A是G的一个模糊子集，如果对于G中的所有x,y，A(x*y-1)≥min(A(x),A(y-1))。类似的泛化原则被用于例如跨度属性的模糊化。设R是X上的一个模糊关系，即R是X×X的一个模糊子集。那么，如果对于X中的所有x，y，z，R(x，z)≥min(R(x，y)，R(y，z))，则R是(模糊-)传递性的。

其他数学科目的类似物已被翻译成模糊数学，如模糊场论和模糊伽罗瓦理论、模糊拓扑学、模糊几何、模糊排序和模糊图。