模糊集运算
编辑模糊集运算是对清晰集运算的概括,适用于模糊集。事实上,可能的概括不止一个。最广泛使用的运算被称为标准模糊集运算;它们包括:模糊补集、模糊交集和模糊联合。
标准模糊集运算
编辑设A和B是模糊集,A,B⊆U,u是U宇宙中的任何元素(如值):u∈U。标准补数一般来说,三联体(i,u,n)被称为DeMorgan三联体,如果i是一个t规范,u是一个t规范(又称s规范),n是一个强否定式,因此,对于所有x,y∈[0,1],以下情况成立。(广义的DeMorgan关系)。这意味着下面详细提供的公理。模糊补体μA(x)被定义为x属于A的程度。让∁A表示类型为c的A的模糊补体,那么μ∁A(x)是x属于∁A的程度,以及x不属于A的程度(因此μA(x)是x不属于∁A的程度)。让一个补充∁A由一个函数定义c:[0,1]→[0,1]对于所有x∈U:μ∁A(x)=c(μA(x))
模糊补充的公理
编辑公理c1.边界条件c(0)=1,c(1)=0公理c2.单调性对于所有a,b∈[0,1],如果a<b,则c(a)>c(b)公理c3.连续性c是连续函数。公理c4.内卷c是一个内卷,这意味着对于每个a∈[0,1],c(c(a))=ac是一个强否定者(又称模糊补充)。一个满足公理c1和c3的函数c至少有一个fixpointa*,c(a*)=a*,如果公理c2也得到满足,则正好有一个这样的fixpoint。对于标准的否定子c(x)=1-x,唯一的费点是a*=0.5。
模糊交集
编辑两个模糊集A和B的交集一般是由单位区间上的二元运算来指定的,这个函数的形式为i:[0,1]×[0,1]→[0,1]。对于所有x∈U:μA∩B(x)=i[μA(x),μB(x)]。
模糊相交的公理
编辑公理i1.边界条件i(a,1)=A公理i2.单调性b≤d意味着i(a,b)≤i(a,d)公理i3.共轭性i(a,b)=i(b,a)公理i4.关联性i(a,i(b,d))=i(i(a,b),d)公理i5.连续性i是一个连续函数公理i6.次幂性i(a,a)<aforall0<a<1公理i7.严格的单调性i(a1,b1)<i(A2,b2)如果a1<a2且b1<b2公理i1到i4定义了一个t-norm(又称模糊相交)。标准的t-normmin是唯一的等值t-norm(也就是说,i(a1,a1)=a对于所有a∈[0,1])。
模糊联盟
编辑两个模糊集A和B的联盟一般由单位区间函数上的二元操作指定,其形式为u:[0,1]×[0,1]→[0,1]。对于所有x∈U:μA∪B(x)=u[μA(x),μB(x)]。
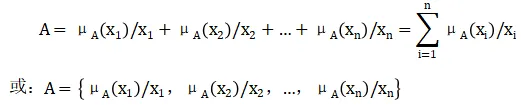
模糊联合的公理
编辑公理u1.边界条件u(a,0)=u(0,a)=a公理u2.单调性b≤d意味着u(a,b)≤u(a,d)公理u3.共轭性u(a,b)=u(b,a)公理u4.关联性u(a,u(b,d))=u(u(a,b),d)公理u5.连续性u是一个连续函数公理u6.超幂性u(a,a)>a对于所有0<a<1公理u7.严格的单调性a1<a2和b1<b2意味着u(a1,b1)<u(a2,b2)公理u1到u4定义了一个t-orm(又称s-orm或模糊联合)。标准的t-conormmax是唯一的empotentt-conorm(即u(a1,a1)=aforalla∈[0,1])。聚合操作模糊集上的聚合操作是将几个模糊集以一种理想的方式结合起来,产生一个单一的模糊集的操作。对n个模糊集(2≤n)的聚集操作由一个函数定义h:[0,1]n→[0,1]。
聚合操作模糊集的公理
编辑公理h1。边界条件h(0,0,…,0)=0,h(1,1,…,1)=1公理h2.单调性对于任何一对<a1,a2,…,an>和<b1,b2,…,bn>的n个元组,如ai,bi∈[0,1],对于所有i∈Nn,如果ai≤bi,对于所有i∈Nn,则h(a1,a2,…,an)≤h(a1,a2,…,an)公理h3.连续性h是一个连续的函数。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/170592/
