身份类型
编辑在类型理论中,身份类型代表平等的概念。它也被称为命题式平等,以区别于判断式平等。类型理论中的平等性是一个复杂的话题,一直是研究的对象,比如同构类型理论领域。
与判断性平等的比较
编辑身份类型是类型理论中两种不同的平等概念之一。更基本的概念是判断性平等,它是一种判断。超越判断性平等身份类型可以做得比判断性平等更多。它可以被用来表明对所有这在判断平等中是不可能显示的。这是通过使用自然数的消除器(或游标)来完成的,称为R。R函数让我们在自然数上定义一个新的函数。这个新函数P被定义为(λx:nat.x+1=1+x)。其他参数的作用类似于归纳证明的部分。参数PZ:P0成为基例0+1=1+0,也就是术语reflnat1。参数PS:Pn→{{dISPlaystyleto}toP(Sn)成为归纳情况。本质上,这说的是当x+1=1+x有x替换成一个规范值时,表达式将与reflnat(x+1)相同。
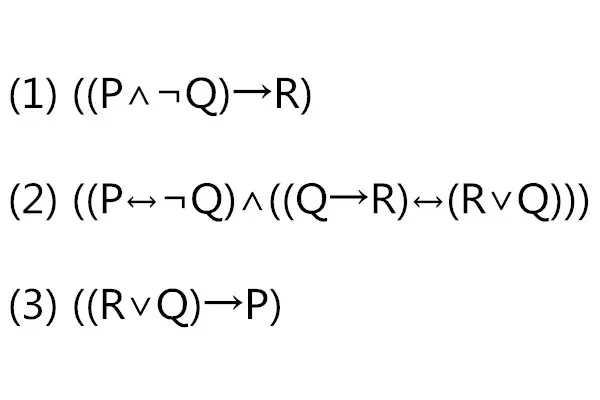
身份类型的版本
编辑身份类型很复杂,是类型理论研究的主题。虽然每个版本都在构造函数上达成了一致,即refl.NAT。它们的属性和消除器函数有很大的不同。对于扩展的版本,任何身份类型都可以转换为判断性的平等。一个计算版本被称为公理K,由于ThomasStreicher的存在。这些最近都不太流行。
身份类型的复杂性
编辑MartinHoffman和ThomasStreicher驳斥了思想类型理论要求身份类型的所有项都是相同的说法。对同一类型的研究的一个流行分支是同构类型理论及其立方体类型理论。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/170657/
