可还原性公理

可还原性公理是由伯特兰-罗素在20世纪初提出的，作为他的类型的ramified理论的一部分。

罗素设计并介绍了公理，试图管理的矛盾，他已经发现在他的分析集合理论。

随着罗素发现（1901年，1902年）戈特洛布-弗雷格的1879年Begriffsschrift中的一个悖论，以及弗雷格对这一悖论的承认（1902年），罗素在1903年的《数学原理》中暂时将他的解决方案作为附录B：类型学说。这个矛盾可以说是所有不包含自己为元素的类的矛盾。在这个附录的末尾，罗素断言他的学说会解决弗雷格提出的直接问题，但至少有一个密切类似的矛盾可能无法通过这个学说解决。所有逻辑对象或所有命题的整体性，似乎涉及一个基本的逻辑困难。

这个困难的完整解决方案可能是什么，我还没有成功地发现；但由于它影响到推理的根本基础......1903年，罗素将预测性函数定义为那些其顺序比函数表达中出现的最高顺序函数多一个的函数。虽然这些对当时的情况来说没有问题，但暗示性函数却不得不被禁止。一个其参数是一个个体并且其值总是一个一阶命题的函数将被称为一阶函数。

一个涉及一阶函数或命题作为表观变量的函数将被称为二阶函数，以此类推。一个变量的函数，如果比它的参数的顺序次之，将被称为谓词函数；同样的名称将被赋予一个多个变量的函数[等等]。他在论文后面以稍微不同的方式重复了这个定义（同时还有一个微妙的禁令，他们将在1913年更清楚地表达）。如果x是一个个体或一个命题，那么x的谓语函数是一个其值为x的下一个类型的命题的函数，如果x是一个函数，那么x的值的函数。

它可以被描述为这样一个函数，其中的表观变量，如果有的话，都是与x相同的类型或较低的类型；如果一个变量可以明显地作为x的参数出现，或作为x的参数的参数，等等，那么它的类型就比x低。[强调是后加的]这种用法一直延续到阿尔弗雷德-诺思-怀特海和罗素1913年的《数学原理》，其中作者在第二章中用了一整个小节。恶性循环原则：我们将把一个变量的函数定义为预言性的，当它比它的参数高一阶时，即与它有该参数相适应的最低阶。

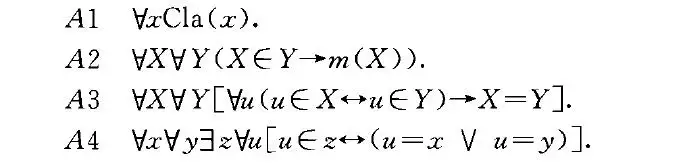
..一个由多个参数组成的函数是谓语性的，如果它有一个参数，当其他参数被赋值时，我们得到一个未确定的参数的谓语性函数。他们再次提出，预测性函数的定义是不违反《逻辑类型理论》的函数。事实上，作者断言这种违反是无法[实现]的，也是不可能的。因此，我们从恶性循环原则和直接检查中得出结论，一个给定的对象a可以作为参数的函数不可能成为彼此的参数，而且它们与可以作为参数的函数没有共同的术语。因此，我们被引导去构建一个层次结构。作者强调了不可能这个词。如果我们没有弄错的话，不仅一个函数φz不可能有它自己或从它派生出来的任何东西作为参数，而且，如果ψz是另一个函数，存在着φa和ψa都有意义的参数a，那么ψz和从它派生出来的任何东西都不能明显地成为φz的参数。

可还原性公理指出，任何真值函数（即命题函数）都可以由一个形式上等同的谓词真值函数来表达。

它在伯特兰-罗素（BertrandRussell）（1908）的《数学逻辑》中首次出现，是以类型理论为基础的，但只是经过了大约五年的试验和错误，用他的话说。

因此，一个个体的谓语函数是一个一阶函数；而对于更高的参数类型，谓语函数取代了一阶函数在个体方面的位置。