简单类型的lambda微积分

简单类型的lambda微积分({displaystyle/lambda{to}}，是类型理论的一种形式。)，是类型理论的一种形式，是λ微积分的类型化解释，只有一个类型构造函数({displaystyleto}）是对λ微积分的类型化解释，它只有一个类型构造函数（→{displaystyleto})来构建函数类型。它是类型化lambda微积分的典型和最简单的例子。简单类型的lambda微积分最初是由AlonzoChurch在1940年提出的，目的是为了避免非类型的lambda微积分的矛盾使用。术语简单类型也被用来指代简单类型的λ微积分的扩展，如积、共积或自然数（系统T），甚至是完全递归（如PCF）。相比之下，引入多态类型（如系统F）或依赖类型（如逻辑框架）的系统不被认为是简单类型的。除了完全递归之外，简单类型仍然被认为是简单的，因为这种结构的教会编码可以只使用{displaystyleto}和合适的类型变量来完成。和合适的类型变量，而多态性和依赖性则不能。

在本文中，符号{displaystylesigmatotau}是指在给定类型输入的情况下的函数类型。指的是函数的类型，即给定一个类型为{displaystylesigma}，产生一个类型为σ的输出。，必须首先被定义。这些有时被称为原子类型或类型常量。在固定了这些之后，类型的语法是：。一组术语常量也被固定为基本类型。例如，它可能假设一个基类型nat，而术语常数可能是自然数。在最初的表述中，Church只使用了两个基类型。{displaystyle`iota}则有一个术语常数。

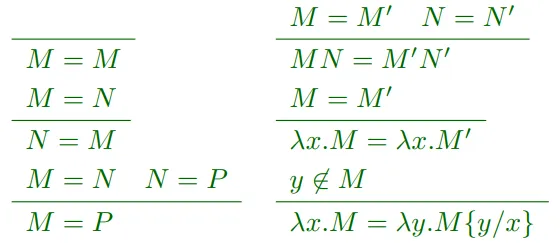
有一个项常数。通常，只有一个基本类型的微积分，通常是简单类型的lambda微积分的语法本质上是lambda微积分本身的语法。术语{displaystylex}的内部，就被绑定了。.如果没有未绑定的变量，那么一个术语就是封闭的。相比之下，无类型的lambdacalculus的语法没有这种类型或术语常量。而在类型化的lambda微积分中，每个抽象（即函数）必须指定其参数的类型。

为了定义一个给定类型的良好类型的λ项的集合，我们将在项和类型之间定义一个类型化关系。首先，我们引入类型化语境或类型化环境).类型化关系的实例被称为类型化判断。一个类型化判断的有效性是通过提供一个类型化推导来显示的，这个推导是用类型化规则构建的（其中线上面的前提允许我们推导出线下面的结论）。简单类型的lambdacalculus使用这些规则。