类型构造器

在被称为类型理论的数理逻辑和计算机科学领域，类型构造器是类型化形式语言的一个特征，它从旧类型中建立新类型。基本类型被认为是使用空类型构造器建立的。一些类型构造器将另一种类型作为参数，例如，积类型、函数类型、幂类型和列表类型的构造器。新的类型可以通过递归地组合类型构造器来定义。例如，简单类型的lambdacalculus可以被看作是一种具有单一非基本类型构造器的语言--函数类型构造器。在类型化的λ计算中，产品类型通常可以通过咖喱被认为是内置的。抽象地讲，类型构造器是一个n-ary类型操作符，它的参数是零或多个类型，并返回另一个类型。利用currying，n-ary类型操作符可以被（重新）写成一元类型操作符的应用序列。因此，我们可以把类型操作符看作是一个简单类型的lambda计算，它只有一个基本类型，通常表示为，以及发音类型，这是基础语言中所有类型的类型，现在被称为适当类型，以区别于类型运算符在自己的微积分中的类型，后者被称为种类。

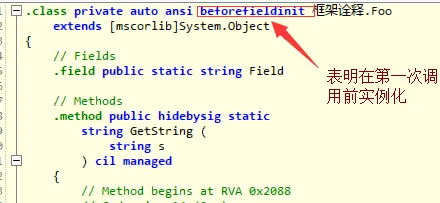
类型运算符可以绑定类型变量。例如，在类型层次上给出简单类型的λ-微积分的结构需要绑定的，或高阶的类型操作符。这些绑定的类型算子对应于λ-立方体的第二轴，以及类型理论，如带有类型算子的简单类型的λ-微积分，λω。将类型操作符与多态的λ-微积分（系统F）结合起来，可以得到系统Fω。