模态逻辑

模态逻辑是为表示关于必然性和可能性的声明而开发的形式系统的集合。它在语言哲学、认识论、形而上学和自然语言语义学中发挥着重要作用。模态逻辑通过增加单数运算符来扩展其他系统分别代表可能性和必然性。例如，模态公式{displaystyle`DiamondP}，可以理解为可能的和必然的。可以被理解为可能.模态逻辑可以用来表示不同的现象，这取决于所考虑的是什么样的必然性和可能性。当在认识论上是必要的，或者换句话说，它是已知的。当{displaystyleBox}被用来表示道义上的必要性。被用来表示道义上的必要性。在模态逻辑的标准关系语义中，公式是相对于一个可能的世界分配真值的。一个公式在一个可能世界的真值可以取决于其他可能世界的其他公式的真值。特别是。{displaystyle/DiamondP}在一个世界中是真的，如果它是在一个世界中。{displaystyleBoxP}在某个世界是真的，如果P{displaystyleBoxP}在某个可访问的可能世界是真的。在每个可接触的可能世界都是真的。

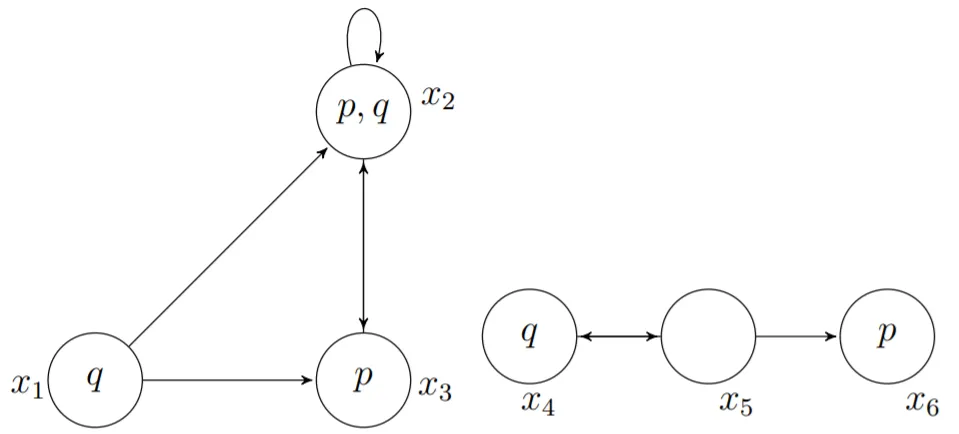
就通过限制可及性关系得到的语义而言，存在各种证明系统是健全和完整的。例如，如果我们要求可及性关系是串行的，那么去定性模态逻辑D就是健全和完整的。虽然模态逻辑背后的直觉可以追溯到古代，但xxx个模态公理系统是由C.I.Lewis在1912年开发的。现在标准的关系语义学是在二十世纪中期由ArthurPrior,JaakkoHintikka和SaulKripke的工作中出现的。最近的发展包括替代的拓扑语义学，如邻域语义学，以及关系语义学在其原始哲学动机之外的应用。这些应用包括博弈论、道德和法律理论、网页设计、基于多元宇宙的集合理论和社会认识论。

模态逻辑与其他类型的逻辑不同，它使用模态运算符，如.前者通常被朗读为必然，可以用来表示道德或法律义务、知识、历史必然性等概念。后者通常被读作可能，可以用来表示包括许可、能力、与证据的兼容性等概念。虽然模态逻辑的良好形成的公式包括非模态公式，如通过引入与上述第4和第5条类似的规则，模态运算符可以被添加到其他种类的逻辑中。模态谓词逻辑是一个广泛使用的变体，包括如下公式因此不需要单独的句法规则来介绍它。然而，在两个运算符不能相互定义的系统中，单独的句法规则是必要的。常见的符号变体包括符号，如{displaystyle{langleKrangle}等符号。在模态逻辑系统中用于表示知识和{displaystyle[B]}