图形切割优化

图形切割优化是一种适用于离散变量函数系列的组合优化方法，以流动网络理论中的切割概念命名。由于xxx流量最小切割定理，确定代表流量网络的图形上的最小切割等同于计算该网络上的xxx流量。给定一个伪布尔函数{displaystylef}，如果有可能构建一个伪布尔函数如果有可能构建一个具有正数权重的流网络，使得在多项式时间内，通过计算图形的最小切面，可以找到f{displaystylef}的全局最优。切割和变量分配之间的映射是通过用图中的一个节点代表每个变量来完成的，给定一个切割，如果相应的节点属于连接到源的组件，则每个变量的值为0，如果属于连接到汇的组件，则为1。并非所有的伪布尔函数都可以用流网络表示，在一般情况下，全局优化问题是NP-hard。存在充分的条件来描述可以通过图切优化的函数家族，如子模四元函数。图形切割优化可以扩展到具有有限数量值的离散变量的函数，可以用具有强优化特性的迭代算法来处理，在每次迭代中计算一个图形切割。图切优化是推断马尔科夫随机场或条件随机场等图形模型的重要工具，它在计算机视觉问题上有应用，如图像分割、去噪、注册和立体匹配。

一个伪布尔函数{displaystyleG=（V,E）}具有非负的权重，并且有源节点和汇节点{displaystylef(x_{1},dots,x_{n})}等于（至多是常数）由最小切割决定的流量值。等于（到一个常数）由最小切割决定的流量值C=(S,T){displaystyleC=(S,T)}相当于图的最小切口C=(S,T){displaystyleG}的最小切割所决定的值。可以根据伪布尔函数的顺序对其进行分类，顺序由每个单项的xxx变量数决定。

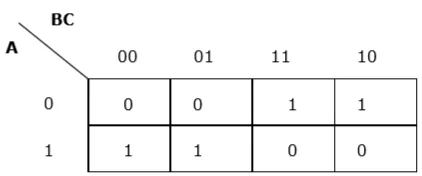
所有一阶函数，即每个项最多取决于一个变量，总是可以表示的。二次函数是可表示的，当且仅当它们是次模态的，即对于每个二次项是可表示的，当且仅当它们是有规律的，即所有可能的二元投影到两个变量，通过固定其余变量的值得到的，都是亚模数。对于高阶函数，规则性是可表示性的一个必要条件。

可表示函数的图形构造因以下事实而简化：两个可表示函数之和{displaystyleG''=(V'',E'')}表示两个函数。代表这两个函数。这样的定理允许建立代表每个术语的独立图形，并将它们结合起来，得到一个代表ent的图形。