主变异搜索

主变异搜索（有时等同于实际上相同的NegaScout）是一种negamax算法，可以比alpha-beta修剪更快。与alpha-beta修剪法一样，NegaScout是一种定向搜索算法，用于计算树中节点的最小值。它主导了alpha-beta修剪，因为它永远不会检查一个可以被alpha-beta修剪的节点；然而，它依赖于准确的节点排序来利用这一优势。当有一个好的移动排序时，NegaScout工作得xxx。在实践中，移动排序往往是由以前较浅的搜索决定的。它通过假设xxx个被探索的节点是xxx的，从而产生比α-β更多的截断。换句话说，它假定xxx个节点在主变异中。然后，它可以通过用空窗口（也称为侦察窗口；当α和β相等时）搜索其余的节点来检查是否是真的，这比用常规的α-β窗口搜索要快。如果证明失败，那么xxx个节点就不在主变体中，然后继续像正常的α-β那样搜索。因此，当移动排序良好时，NegaScout工作得xxx。在随机移动排序的情况下，NegaScout将比普通的alpha-beta花费更多的时间；尽管它不会探索alpha-beta没有探索过的任何节点，但它将不得不重新搜索许多节点。AlexanderReinefeld在α-beta剪枝法发明几十年后发明了NegaScout。他在他的书中给出了NegaScout的正确性证明。另一种叫做SSS*的搜索算法在理论上可以使搜索的节点更少。然而，它的原始表述有实际问题（特别是它在很大程度上依赖于OPEN列表的存储），现在大多数国际象棋引擎仍然在搜索中使用NegaScout的一种形式。大多数国际象棋引擎使用一个换位表，搜索树的相关部分被储存在其中。这一部分树的大小与SSS*的OPEN列表相同。一个被称为MT-SSS*的重构允许它被实现为一系列对Alpha-Beta（或NegaScout）的空窗调用，这些调用使用换位表，并且可以使用游戏程序进行直接比较。它在实践中并没有超过NegaScout的表现。然而，另一种搜索算法，在实践中确实倾向于比NegaScout做得更好，是称为MTD(f)的最佳优先算法，尽管这两种算法都没有支配对方。在一些树上，NegaScout搜索的节点比SSS*或MTD(f)少，反之亦然。NegaScout采用了JudeaPearl在1980年发明的SCOUT，它是xxx个优于alpha-beta并被证明是渐进最优的算法。空窗，在negamax设置中β=α+1，是由J.P.Fishburn独立发明的，并在他的博士论文的附录中用于类似于SCOUT的算法，在一个并行的alpha-beta算法中，以及在搜索树根节点的最后一个子树上。

大多数棋步对双方来说都是不可接受的，所以我们不需要完全搜索每个节点来获得确切的分数。准确的分数只需要在主要变化中（一连串双方都能接受的棋步），预计会向下传播到根。在迭代深化搜索中，前一次迭代已经建立了这样一个序列。在一个分数最终在窗口内的节点，也就是所谓的PV-节点，我们在一个完整的窗口中搜索被认为是xxx的xxx步棋，以建立一个约束。这需要证明其他动作是不可接受的。

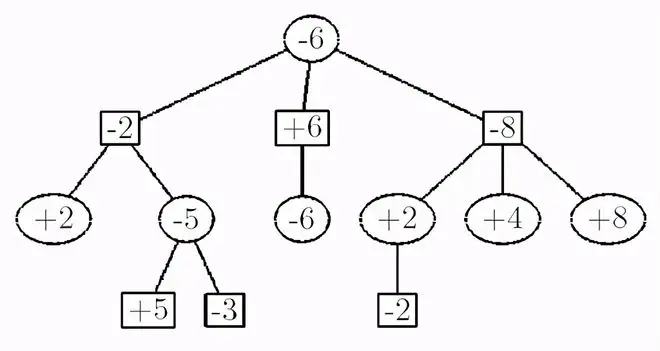
我们进行了一个零窗口搜索，以测试一个动作是否可以更好。由于零窗口搜索要便宜得多，它可以节省大量的精力。如果我们发现某一步棋可以提高阿尔法，我们就用全窗口重新搜索，以得到准确的分数。伪码函数pvs(node,depth,α,β,color)是如果深度=0或节点是终端节点，则返回颜色×节点的启发式数值，对于节点的每个子节点，如果子节点是xxx个子节点，则得分:=-pvs(child,depth-1,-β,-α,-color)否则得分:=-pvs(child,depth-1,-α-1,-α,-color)(*用空窗口搜索*)如果α<score<β则score:=-pvs(child,depth-1,-β,-score,-color)(*如果失败率高，则做全面的重新搜索*)α:=max(α,score)如果α≥β则break(*β切断*)returnα