降维

降维，或称降维，是指将数据从高维空间转换到低维空间，使低维表示保留原始数据的一些有意义的属性，最 好是接近其固有维度。

由于许多原因，在高维空间工作是不可取的；由于维度诅咒的结果，原始数据往往是稀疏的，而且分析数据通常在计算上是难以解决的（难以控制或处理）。

降维在处理大量观测数据和/或大量变量的领域很常见，如信号处理、语音识别、神经信息学和生物信息学。方法通常被分为线性和非线性方法；方法也可分为特征选择和特征提取。

降维可用于降噪、数据可视化、聚类分析，或作为中间步骤来促进其他分析。

特征选择方法试图找到输入变量的一个子集（也称为特征或属性）。

这三种策略是：过滤策略（如信息增益）、包裹策略（如以准确性为指导的搜索）和嵌入策略（在建立模型时根据预测误差添加或删除所选特征）。

诸如回归或分类等数据分析可以在缩小的空间中比在原始空间中更准确地完成。

特征投射（也叫特征提取）将数据从高维空间转换到一个较少维度的空间。

数据转换可能是线性的，如主成分分析（PCA），但也存在许多非线性降维技术。

对于多维数据，张量表示可以通过多线性子空间学习用于降维。主成分分析（PCA）主要的线性降维技术，主成分分析，将数据线性映射到低维空间，其方式是使数据在低维表示中的方差最大化。

在实践中，数据的协方差（有时是相关）矩阵被构建出来，并计算出该矩阵的特征向量。与xxx特征值相对应的特征向量（主成分）现在可以用来重建原始数据方差的很大一部分。

此外，前几个特征向量往往可以用系统的大规模物理行为来解释，因为它们往往贡献了系统的绝大部分能量，特别是在低维系统中。尽管如此，这必须逐一证明，因为并非所有系统都表现出这种行为。

原始空间（维度为点的数量）已被减少（有数据损失，但希望能保留最重要的方差）到由几个特征向量跨越的空间。

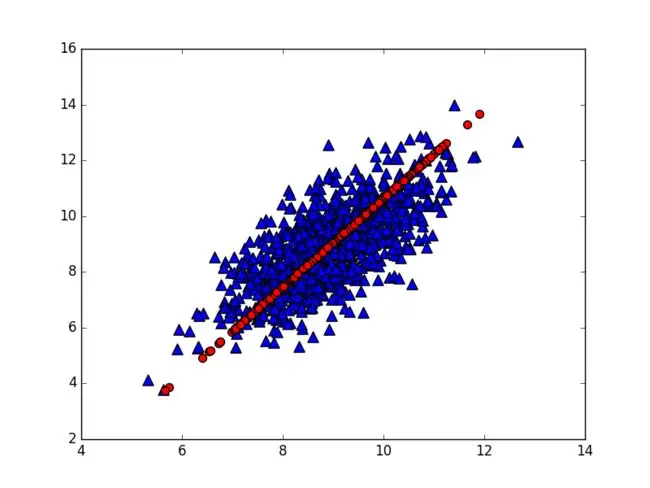
非负矩阵分解（NMF）NMF将一个非负矩阵分解为两个非负矩阵的乘积，这在只有非负信号存在的领域，如天文学，是一个很有前途的工具。

自Lee&Seung的乘法更新规则以来，NMF已广为人知，它得到了不断的发展：包括不确定性，考虑缺失数据和并行计算，顺序构造导致NMF的稳定性和线性，以及其他更新，包括处理数字图像处理中的缺失数据。

由于在构建过程中具有稳定的分量基础，以及线性建模过程，顺序NMF能够在天文学中的环星结构直接成像中保持通量，作为探测系外行星的方法之一，特别是对于环星盘的直接成像。

与PCA相比，NMF没有去除矩阵的平均值，这就导致了不切实际的非负流量；因此NMF能够比PCA保留更多的信息，正如Ren等人所证明的。

主成分分析可以通过核子技巧以非线性方式使用。由此产生的技术能够构建非线性映射，使数据的方差xxx化。由此产生的技术被称为内核PCA。

其他突出的非线性技术包括流形学习技术，如Isomap、局部线性嵌入（LLE）、HessianLLE、Laplacian特征图，以及基于切线空间分析的方法。

这些技术利用保留数据局部属性的成本函数构建了一个低维数据表示，并可被视为为内核PCA定义了一个基于图形的内核。

最近，人们提出了一些技术，这些技术不是定义一个固定的核，而是试图使用半透明的方法来学习核。