自动微分
编辑在数学和计算机代数中,自动微分 (AD) 也称为算法微分、计算微分、自动微分或简称为 autodiff,是一组计算计算机程序指定函数的导数的技术。 AD 利用了这样一个事实,即每个计算机程序,无论多么复杂,都会执行一系列基本算术运算(加法、减法、乘法、除法等)和基本函数(exp、log、sin、cos 等)。 通过对这些运算重复应用链式法则,可以自动计算任意阶的导数,精确到工作精度,并且最多使用比原始程序多一个小常数因子的算术运算。
自主微分不同于符号微分和数值微分。 符号微分面临着将计算机程序转换为单一数学表达式的困难,并可能导致代码效率低下。 数值微分(有限差分法)会在离散化过程和抵消过程中引入舍入误差。 这两种经典方法在计算高阶导数时都存在问题,复杂度和误差都会增加。 最后,这两种经典方法在计算函数相对于许多输入的偏导数时都很慢,而这正是基于梯度的优化算法所需要的。 自动微分解决了所有这些问题。
链式法则,正向和反向积累
编辑AD 的基础是由链式法则提供的微分分解。
通常,存在两种不同的 AD 模式,正向积累(或正向模式)和反向积累(或反向模式)。 前向累积指定从内到外遍历链式规则(即首先计算 d w 1 / d x {dISPlaystyle dw_{1}/dx} 然后 d w 2 / d w 1 {diSPlaystyle dw_{2}/ dw_{1}} 最后是 d y / d w 2 {displaystyle dy/dw_{2}} ),而反向累加则是从外到内遍历(先计算 d y / d w 2 {displaystyle dy/dw_{ 2}} 然后 d w 2 / d w 1 {displaystyle dw_{2}/dw_{1}} 最后是 d w 1 / d x {displaystyle dw_{1}/dx} )。
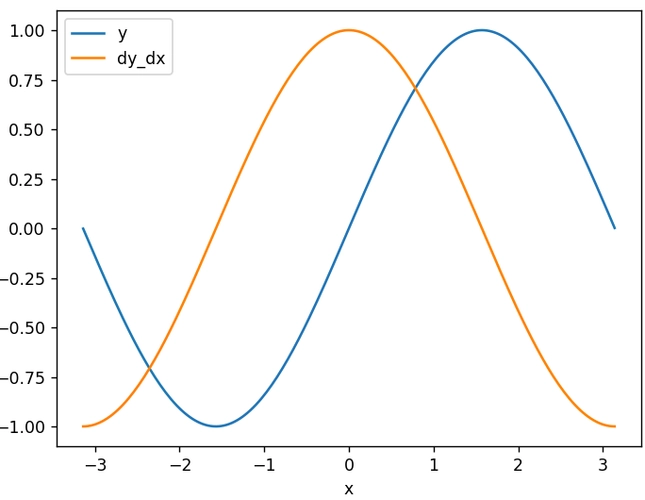
正向积累
编辑在前向累加AD中,首先固定进行微分的自变量,递归地计算每个子表达式的导数。 在纸笔计算中,这涉及重复代入链式法则中的内部函数的导数,与逆向累加相比,正向累加自然且易于实现,因为衍生信息的流动与评估顺序一致。 每个变量 w 都增加了它的导数 ẇ(存储为数值,而不是符号表达式)。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/193409/
