时不变系统

在控制理论中，时不变 (TIV) 系统具有随时间变化的系统函数，该函数不是时间的直接函数。 此类系统在系统分析领域被视为一类系统。 时变系统函数是时变输入函数的函数。 如果此函数仅间接依赖于时域（例如，通过输入函数），则该系统将被视为时不变的。 相反，任何直接依赖于时域的系统函数都可以被视为时变系统。

从数学上讲，系统的时不变性是以下属性：

给定一个具有随时间变化的输出函数 y ( t ) {\displaystyle y(t)} 和随时间变化的输入函数 x ( t ) {\displaystyle x(t)} 的系统，系统将被视为 如果输入 x ( t + δ ) {\displaystyle x(t+\delta )} 的时间延迟直接等于输出 y ( t + δ ) {\displaystyle y (t+\delta )} 函数。

在信号处理语言中，如果系统的传递函数不是时间的直接函数，除非由输入和输出表示，则可以满足此属性。

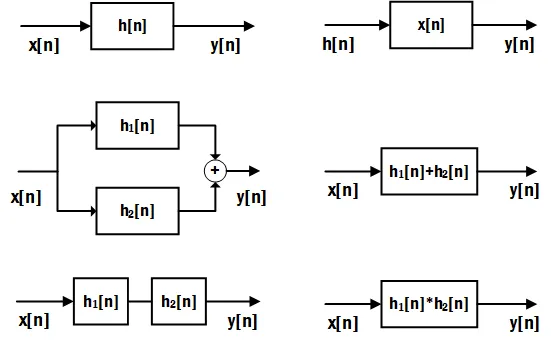
在系统原理图的上下文中，该属性也可以表述如下，如右图所示：

如果系统是时不变的，则系统块会以任意延迟进行通勤。

如果一个时不变系统也是线性的，那么它就是线性时不变理论（linear time-invariant）的主题，在核磁共振波谱、地震学、电路、信号处理、控制理论等技术领域有直接的应用。 非线性时不变系统缺乏综合的、支配性的理论。 离散时不变系统被称为移不变系统。 缺乏时不变性的系统被研究为时变系统。

为了演示如何确定系统是否时不变，

由于系统 A 的系统函数 y ( t ) {\displaystyle y(t)} 明确依赖于 x ( t ) {\displaystyle x(t)} 之外的 t，因此它不是时不变的，因为时间- 依赖性不是输入函数的明确函数。

相反，系统 B 的时间依赖性只是时变输入 x ( t ) {\displaystyle x(t)} 的函数。 这使得系统 B 是时不变的。

下面的形式示例更详细地表明，虽然系统 B 是作为时间 t 的函数的平移不变系统，但系统 A 不是。

现在给出为什么上述系统 A 和 B 不同的更正式的证明。 为了执行此证明，将使用第二个定义。

现在将输出延迟 δ {\displaystyle \delta }

对于时不变系统，系统属性随时间保持不变。