梅特卡夫定律

梅特卡夫定律指出，电信网络的价值与系统连接用户数的平方 (n2) 成正比。

梅特卡夫定律描述了互联网、社交网络和万维网等通信技术和网络的许多网络效应。 美国联邦通信委员会前主席里德·亨特说，这部法律最能理解互联网的运作方式。 梅特卡夫定律与这样一个事实有关，即在一个由 n {displaystyle n} 个节点组成的网络中，xxx可能的连接数可以数学上表示为三角数 n ( n − 1 ) / 2 {displaystyle n (n-1)/2} ，与 n 2 {displaystyle n{2}} 渐进成正比。

这个规律经常用传真机的例子来说明：一台传真机是没有用的，但是每台传真机的价值随着网络中传真机总数的增加而增加，因为每个用户可能与之打交道的总人数 发送和接收文件增加。 同样，在社交网络中，使用该服务的用户数量越多，该服务对社区的价值就越大。

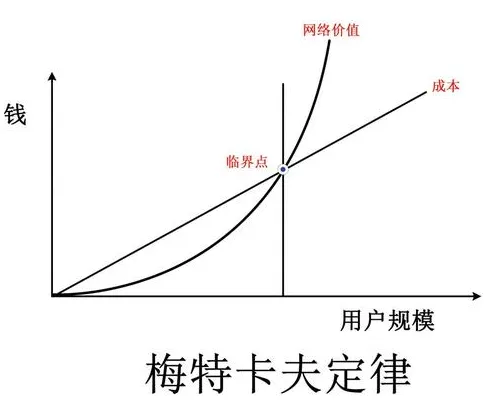
最初的化身小心地在线性成本 (Cn)、非线性增长 n2 和非常量比例因子 A“亲和力”之间划定界限。

在某种规模下，等式右侧 V“价值”超过成本，A 描述规模与净增加值之间的关系。

Metcalfe 将 A 恰当地定义为“每个用户的价值”。 亲和力也是网络规模的函数，Metcalfe 正确地断言 A 必须随着 n 变大而下降。

“可能存在网络规模的不经济，最终会随着规模的增加而压低价值。 因此，如果 V=A*n2，则可能是 A（表示“亲和力”，每个连接的价值）也是 n 的函数，并且在达到一定网络规模后会下降，压倒 n2。”

网络规模和价值不会无限制地增长，而是受到基础设施、技术获取和有限理性（如邓巴数）等实际限制的限制。 用户增长 n 几乎总是达到饱和点。 技术、替代品、竞争对手和技术过时限制了 n 的增长。 通常假定 n 的增长遵循 S 型函数，例如逻辑曲线或 Gompertz 曲线。

A 还受网络拓扑的连通性或密度支配。 在无向网络中，每条边连接两个节点，因此每条边有 2m 个节点。 实际接触的节点比例由 c = 2 m / n {displaystyle c=2m/n} 给出。

简单网络（即没有多边或自边的网络）中边的xxx可能数量是 ( n 2 ) = n ( n − 1 ) / 2 {displaystyle {binom {n}{2 }}=n(n-1)/2} 。 因此，网络的密度 ρ 是实际存在的那些边的部分

梅特卡夫定律假定每个节点 n {displaystyle n} 的价值都是平等的。 如果不是这种情况，例如因为一台传真机为一家公司的 60 名员工提供服务，第二台传真机为其中的一半服务，第三台为三分之一，依此类推，那么额外连接的相对价值就会降低。 同样，在社交网络中，如果后来加入的用户比早期采用者更少地使用网络，那么每个额外用户的收益可能会减少，如果每个用户的成本是固定的，则整个网络的效率就会降低。

在社交网络的背景下，包括梅特卡夫本人在内的许多人提出了修改模型，其中网络的价值增长为 n log ⁡ n {displaystyle nlog n} 而不是 n 2 {displaystyle n{ 2}} 。 Reed 和 Andrew Odlyzko 在描述以下关系方面寻找了与梅特卡夫定律的可能关系。