NP完全

在计算复杂性理论中，一个问题在以下情况下是 NP 完全的：

• 这是一个可以快速验证每个解的正确性的问题（即在多项式时间内），并且暴力搜索算法可以通过尝试所有可能的解来找到解。
• 该问题可用于模拟我们可以快速验证解决方案是否正确的所有其他问题。 从这个意义上说，NP 完全问题是解决方案可以快速验证的最难的问题。 如果我们能快速找到某些 NP 完全问题的解决方案，我们就能快速找到所有其他问题的解决方案，而给定的解决方案可以很容易地得到验证。

名称 NP-complete 是非确定性多项式时间完成的缩写。 在这个名称中，非确定性指的是非确定性图灵机，这是一种在数学上形式化蛮力搜索算法思想的方法。 多项式时间是指确定性算法检查单个解决方案或非确定性图灵机执行整个搜索被认为快速的时间量。 完全是指能够模拟同一复杂度等级中的所有事物的属性。

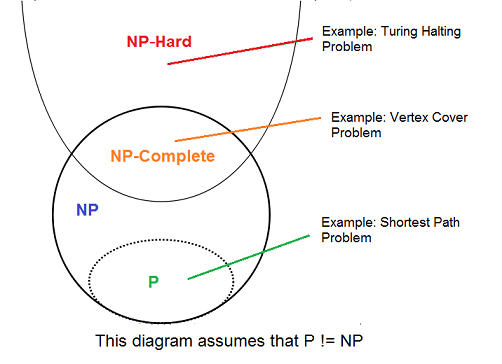
更准确地说，问题的每个输入都应与一组多项式长度的解相关联，其有效性可以快速测试（在多项式时间内），这样如果解集非空且任何输入的输出为是 不，如果它是空的。 这种形式的复杂问题称为 NP，它是非确定性多项式时间的缩写。 如果 NP 中的所有内容都可以在多项式时间内转换为该问题，则该问题被称为 NP-hard，即使它可能不在 NP 中。 相反，如果一个问题同时属于 NP 和 NP-hard，则该问题是 NP-complete。 NP 完全问题代表了 NP 中最难的问题。 如果某些 NP 完全问题具有多项式时间算法，则 NP 中的所有问题都具有。 一组 NP 完全问题通常用 NP-C 或 NPC 表示。

尽管可以快速验证 NP 完全问题的解决方案，但还没有已知的快速找到解决方案的方法。 也就是说，随着问题规模的增长，使用任何当前已知的算法解决问题所需的时间会迅速增加。 因此，确定是否有可能快速解决这些问题（称为 P 与 NP 问题）是当今计算机科学中尚未解决的基本问题之一。

虽然快速计算 NP 完全问题的解决方案的方法仍未被发现，但计算机科学家和程序员仍然经常遇到 NP 完全问题。 NP 完全问题通常通过使用启发式方法和近似算法来解决。

NP-complete 问题是 NP 中的所有决策问题的集合，其解决方案可以在多项式时间内得到验证； NP 可以等效地定义为可以在非确定性图灵机上在多项式时间内解决的决策问题集。 如果 NP 中的所有其他问题都可以在多项式时间内转换（或减少）为 p，则 NP 中的问题 p 是 NP 完全问题。

不知道是否所有 NP 问题都可以快速解决——这称为 P 对 NP 问题。 但是如果任何 NP 完全问题都可以快速解决，那么 NP 中的每个问题都可以，因为 NP 完全问题的定义表明 NP 中的每个问题都必须可以快速还原为每个 NP 完全问题（也就是说，它可以 在多项式时间内减少）。 正因为如此，人们常说 NP 完全问题比一般的 NP 问题更难或更难。

这个定义的结果是，如果我们有 C {displaystyle scriptstyle C} 的多项式时间算法（在 UTM 或任何其他图灵等效抽象机上），我们可以在多项式时间内解决 NP 中的所有问题 .

NP 完全的概念是在 1971 年引入的（参见 Cook-Levin 定理），尽管 NP 完全这个术语是后来引入的。 在 1971 年的 STOC 会议上，计算机科学家之间就是否可以在确定性图灵机上在多项式时间内解决 NP 完全问题展开了激烈的争论。 John Hopcroft 使会议上的每个人都达成共识，即 NP 完全问题是否可以在多项式时间内解决的问题应该推迟到以后解决。