剪切带 (材料工程)

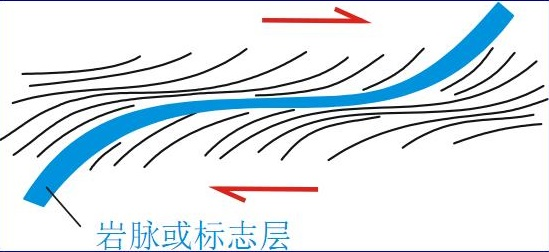
剪切带是强烈剪切应变的狭窄区域，通常具有塑性，在韧性材料的严重变形过程中形成。例如，土壤（超固结的粉质粘土 ) 试样在轴对称压缩试验。 最初样品是圆柱形的，由于在测试过程中试图保持对称性，所以在测试过程中圆柱形保持了一段时间并且变形是均匀的，但是在极限载荷下形成了两个X形剪切带并且 随后的变形是强烈局部化的。

虽然在脆性材料（例如室温下的玻璃）中观察不到，但剪切带或更普遍的“局部变形”通常在广泛的延展性材料（合金、金属、颗粒材料、塑料、聚合物和土壤）中出现 甚至在准脆性材料（混凝土、冰、岩石和一些陶瓷）中。剪切带现象的相关性在于它们先于失效，因为剪切带内发生的极端变形会导致强烈的损坏和断裂。 因此，剪切带的形成是理解延性材料失效的关键，这对于新材料的设计和极端条件下现有材料的开发具有重要意义。 因此，自 20 世纪中叶以来，变形的局部化一直是密集研究活动的焦点。

剪切带（材料工程）形成是材料不稳定性的一个例子，对应于固体样品中发生的变形均匀性的突然丧失，该加载路径与持续均匀变形相容。 从这个意义上说，它可以被解释为一种变形机制“替代”到一个微不足道的变形机制，因此是一个“完美”平衡路径的分叉或独特性的丧失。 这种分叉的显着特征是它甚至可能发生在无限大的物体中（或在光滑接触与刚性约束的极端约束下）。

考虑一个由非线性材料组成的无限体，它以一种应力和应变可能保持均匀的方式发生准静态变形。 为简单起见，假定这种非线性材料的增量响应是线性的，因此它可以表示为应力增量 σ 和应变增量 ε ˙，通过四阶本构张量 C

作为

(1)

其中四阶本构张量 C 取决于当前状态，即当前应力、当前应变和可能的其他本构参数（例如，金属的硬化变量，或 颗粒材料的密度）。

寻找在增量应力和应变中出现不连续表面的条件。 这些条件等同于发生局部变形的条件。 特别是，增量平衡要求增量牵引力（而不是压力！）保持连续

(2)

（其中 + 和 - 表示表面的两侧）和几何相容性对增量应变的形式施加了应变相容性限制：

(3)

其中符号 ⊗ 表示张量积，g 是定义变形不连续模式的向量。 将增量本构法则 (1) 和应变相容性 (3) 代入增量牵引力 (2) 的连续性可得出应变局部化的必要条件：

(4)

是所谓的“声学张量”，定义了加速度波的传播条件，我们可以得出结论，应变局部化的条件与加速度波的奇异性（零速传播）条件一致。 这种情况代表了所谓的控制速率平衡的微分方程的“椭圆度损失”。

剪切带研究的最新进展是从理论和实验的角度很好地理解了这种现象，可用的本构模型给出了很好的定性预测。