在逐步增长的聚合反应中，卡罗瑟斯方程（或 Carothers 方程）给出了聚合度 Xn，对于给定的分数单体转化率 p。

这个方程式有多个版本，由 1935 年发明尼龙的 Wallace Carothers 提出。

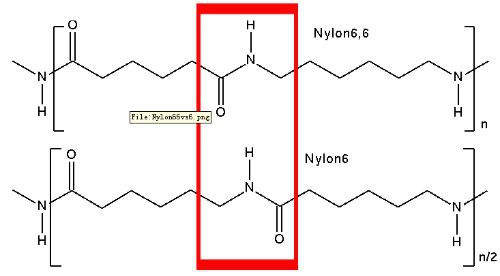
最简单的情况是指通过等摩尔量的两种单体反应（通常通过缩合）形成严格线性的聚合物。 一个例子是尼龙 6,6 的合成

在这个等式中

• X ¯ n {dISPlaystyle {bar {X}}_{n}} 是聚合度的数均值，等于聚合物分子中单体单元的平均数。
• p = N 0 − N N 0 {diSPlaystyle p={tfrac {N_{0}-N}{N_{0}}}} 是反应（或转化为聚合物）的程度，定义为
  • N 0 {displaystyle N_{0}} 是最初作为单体存在的分子数
  • N {displaystyle N} 是时间 t 后出现的分子数。 总数包括所有聚合度：单体、低聚物和聚合物。

该方程表明，需要高单体转化率才能实现高聚合度。

线性聚合物：一种单体过量

如果一种单体以化学计量过量存在

r是反应物的化学计量比，过量的反应物通常是分母，使得r＜1。 1. 如果两个单体都不过量，则 r = 1，方程式简化为上述等摩尔情况。

对于给定的 p 值，过量反应物的作用是降低聚合度。 在限制试剂单体完全转化的极限下

因此，对于 1% 过量的一种单体，r = 0.99，聚合极限度为 199，而等摩尔情况下为无穷大。 可以使用过量的一种反应物来控制聚合度。

单体分子的官能度是参与聚合的官能团的数量。 官能度大于两个的单体会在聚合物中引入支化，聚合度将取决于每个单体单元的平均官能度。 对于初始含有 N0 个分子且两个官能团 A 和 B 数量相等的体系，官能团总数为 N0fav。

与卡罗瑟斯方程相关的是以下方程式（对于由等摩尔量的两种单体形成的线性聚合物的最简单情况）

在哪里：

• Xw为重均聚合度，
• Mn为数均分子量，
• Mw为重均分子量，
• Mo为重复单体单元的分子量，
• Đ 是分散指数。 （原名多分散指数，符号PDI）

最后一个等式表明 Đ 的最大值为 2，这发生在单体转化率为 100%（或 p = 1）时。 这适用于线性聚合物的逐步增长聚合。 对于链增长聚合或支化聚合物，Đ 可以高得多。

在实践中，聚合物链的平均长度受到反应物纯度、不存在任何副反应（即高产率）和介质粘度等因素的限制。