Youla-Kucera参数化

在控制理论中，Youla–Kučera 参数化（也简称为 Youla 参数化）是一个公式，它描述了给定对象 P 的所有可能的稳定反馈控制器，作为单个参数 Q 的函数。

YK 参数化是一般结果。 它是控制理论的一项基本成果，开辟了一个全新的研究领域，并在优化和鲁棒控制等方面找到了应用。 YK公式的工程意义在于，如果想找到一个满足某些附加准则的稳定控制器，可以通过调整参数Q来满足期望的准则。

为了便于理解，正如 Kučera 所建议的那样，xxx描述三种越来越普遍的植物。

令 P ( s ) {displaystyle P(s)} 为稳定的单输入单输出系统 (SISO) 系统的传递函数。 此外，令 Ω {displaystyle Omega } 为 s {displaystyle s} 的一组稳定且适当的函数。

考虑具有传递函数 P ( s ) {displaystyle P(s)} 的一般植物。

其中要找到的变量 ( X ( s ) , Y ( s ) ) {displaystyle (X(s),Y(s))} 也必须适当且稳定。

在找到合适且稳定的 X , Y {displaystyle X,Y} 之后，我们可以定义一个稳定控制器，其形式为 C ( s ) = Y ( s ) X ( s ) {displaystyle C(s) ={frac {Y(s)}{X(s)}}} 。 在我们手头有一个稳定控制器之后，我们可以使用适当且稳定的参数 Q ( s ) {displaystyle Q(s)} 来定义所有稳定控制器。

在多输入多输出 (MIMO) 系统中，考虑传输矩阵 P ( s ) {displaystyle mathbf {P(s)} } 。 它可以使用右互质因式分解 P ( s ) = N ( s ) D − 1 ( s ) {displaystyle mathbf {P(s)=N(s)D{-1}(s)} } 或左因子 P ( s ) = D ~ − 1 ( s ) N ~ ( s ) {displaystyle mathbf {P(s)={波浪号 {D}}{-1}(s){ 波浪号 {N}}(s)} } 。 这些因子必须是适当的、稳定的和双互质的，这确保系统 P ( s ) {displaystyle mathbf {P(s)} } 是可控和可观察的。

在找到稳定且适当的 X , Y , X ~ , Y ~ {displaystyle mathbf {X,Y,{tilde {X}},{tilde {Y}}} } 之后，我们可以 使用左因子或右因子定义所有稳定控制器 K ( s ) {displaystyle mathbf {K(s)} } 的集合，前提是有负反馈。

其中 Δ {displaystyle Delta } 是任意稳定且适当的参数。

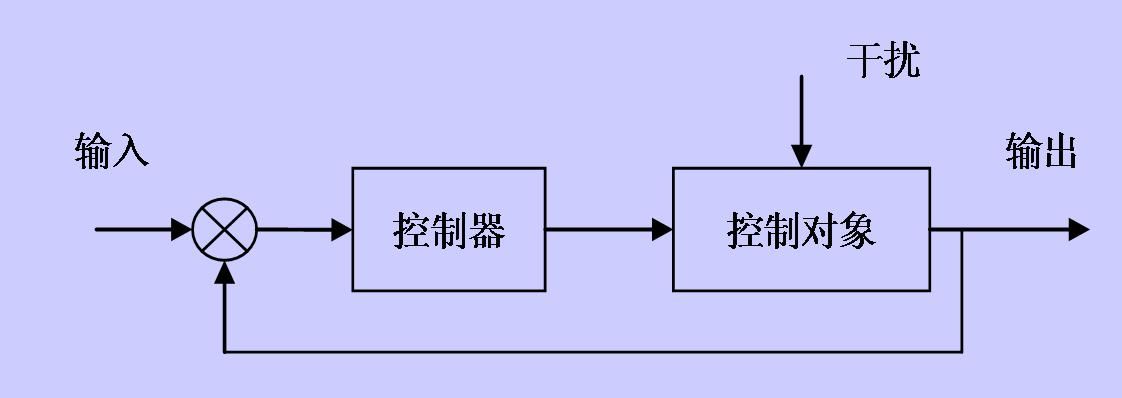
设 P ( s ) {displaystyle P(s)} 为设备的传递函数，设 K 0 ( s ) {displaystyle K_{0}(s)} 为稳定控制器。