截面 (几何)

在几何学和科学中，横截面是三维空间中的实体与平面或更高维空间中的类比的非空交集。 将物体切成薄片会产生许多平行的横截面。 三维空间中平行于两个轴的截面的边界，即平行于由这些轴确定的平面的边界，有时被称为等高线； 例如，如果一个平面穿过与地面平行的凸起浮雕地图的山脉，则结果是二维空间中的等高线，显示等高山表面上的点。

在技术绘图中，横截面是物体在与其相交的平面上的投影，是一种常用工具，用于在二维中描绘 3 维物体的内部排列。 它传统上是交叉影线，交叉影线的样式通常表示所使用的材料类型。

通过计算机轴向断层扫描，计算机可以根据 X 射线数据构建横截面。

如果平面与实体（3 维对象）相交，则平面和实体的公共区域称为实体的横截面。 包含固体横截面的平面可称为切割平面。

实体横截面的形状可能取决于切割平面相对于实体的方向。 例如，虽然球的所有横截面都是圆盘，但立方体的横截面取决于切割平面与立方体的关系。 如果切割平面垂直于连接立方体两个相对面的中心的线，则横截面将为正方形，但是，如果切割平面垂直于连接相对顶点的立方体的对角线，则横截面 截面可以是一个点、一个三角形或一个六边形。

一个相关的概念是平面截面，它是平面与表面相交的曲线。 因此，平面截面是切割平面中固体横截面的边界。

如果三维空间中的表面由两个变量的函数定义，即 z = f(x, y)，则平面由平行于坐标平面（由两个坐标轴确定的平面）的切割平面分割 ) 称为水平曲线或等值线。更具体地说，具有 z = k 形式的方程的切割平面（平行于 xy 平面的平面）产生的平面截面在应用领域通常称为等高线。

多面体的横截面是多边形。

圆锥截面——圆、椭圆、抛物线和双曲线——是圆锥的平面截面，其切割平面处于不同的角度，如左图所示。

任何通过椭球中心的截面都构成一个椭圆区域，而相应的平面截面在其表面上都是椭圆。 当切割平面垂直于对称轴时，它们分别退化为圆盘和圆。 更一般地说，二次曲面的平面截面是圆锥截面。

如果横截面平行于圆柱体的底面，则在两个底面之间延伸的实心直立圆柱体的横截面是圆盘，如果既不平行也不垂直于圆柱体的底面，则为椭圆区域（见右图） 基地。 如果切割平面垂直于底部，则它由一个矩形（未显示）组成，除非它刚好与圆柱相切，在这种情况下它是一条线段。

术语圆柱体也可以表示实心圆柱体的侧面（参见圆柱体（几何））。 如果在这个意义上使用圆柱体，则上段内容如下：如果切割平面垂直于圆柱体的对称轴，则有限长度的直立圆柱体的平面截面为圆形，或者为椭圆形 如果它既不平行也不垂直于该轴。 如果切割平面平行于轴，则平面截面由一对平行线段组成，除非切割平面与圆柱相切，在这种情况下，平面截面是一条线段。

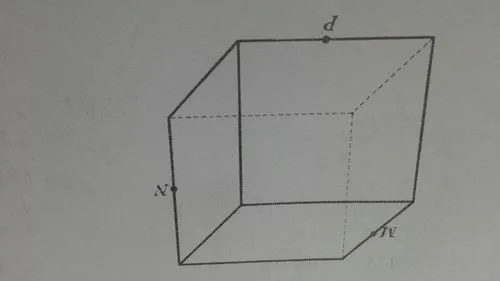
如图所示，平面截面可用于可视化函数关于其参数之一的偏导数。 假设 z = f(x, y)。 在求 f(x, y) 对 x 的偏导数时，可以取函数 f 在 y 的固定值处的平面截面来绘制 z 单独对 x 的水平曲线； 那么关于 x 的偏导数就是所得二维图的斜率。

两个随机变量的概率密度函数的平面截面，其中切割平面在其中一个变量的固定值处是另一个变量的条件密度函数（以定义平面截面的固定值为条件）。