正则变换生成函数

在物理学中，更具体地说，在哈密顿力学中，生成函数是松散的函数，其偏导数生成决定系统动力学的微分方程。 常见的例子有统计力学的配分函数、哈密顿量，以及在执行规范变换时充当两组规范变量之间的桥梁的函数。

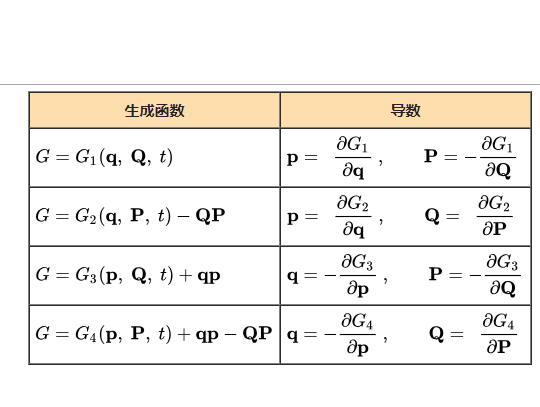
有四种基本的生成函数，总结如下表：

有时，给定的哈密顿量可以变成一个看起来像谐振子哈密顿量的哈密顿量，即

H = a P 2 + b Q 2 。 {displaystyle H=aP{2}+bQ{2}.}

例如，哈密顿量

H = 1 2 q 2 + p 2 q 4 2 , {displaystyle H={frac {1}{2q{2}}}+{frac {p{2}q{4}}{2 }},}

其中 p 是广义动量，q 是广义坐标，一个好的规范变换可以选择

(1)

这将哈密顿量变成

H = Q 2 2 + P 2 2 , {displaystyle H={frac {Q{2}}{2}}+{frac {P{2}}{2}},}

这是谐振子哈密顿量的形式。

该变换的生成函数 F 属于第三类，

F = F 3 (p, Q)。 {displaystyle F=F_{3}(p,Q).}

要明确找到 F，请使用上表中的导数方程式，

P = − ∂ F 3 ∂ Q , {displaystyle P=-{frac {partial F_{3}}{partial Q}},}

将等式（1）中P的表达式代入，用p和Q表示：

p Q 2 = − ∂ F 3 ∂ Q {displaystyle {frac {p}{Q{2}}}=-{frac {partial F_{3}}{partial Q}} }

将其与 Q 进行积分，得到等式 (1) 给出的变换生成函数的等式：

要确认这是正确的生成函数，请验证它是否匹配 (1)：

q = − ∂ F 3 ∂ p = − 1 Q {displaystyle q=-{frac {partial F_{3}}{partial p}}={frac {-1}{Q }}}