简介
编辑在数学中,在研究具有二维相空间的动力系统时,极限环是相空间中的一条闭合轨迹,其特性是随着时间接近无穷大或时间接近负无穷大,至少有一条其他轨迹盘旋进入其中。 这种行为在一些非线性系统中表现出来。 极限环已被用于模拟许多现实世界振荡系统的行为。 极限环的研究是由 Henri Poincaré (1854–1912) 发起的。
定义
编辑我们考虑形式为 x ′ ( t ) = V ( x ( t ) ) {dISPlaystyle x'(t)=V(x(t))} 的二维动力系统,其中 V : R 2 → R 2 {diSPlaystyle V:mathbb {R} {2}to mathbb {R} {2}} 是平滑函数。 这个系统的轨迹是一些平滑函数 x ( t ) {displaystyle x(t)} 其值在 R 2 {displaystyle mathbb {R} {2}} 满足这个微分方程。 如果这样的轨迹不是恒定的而是返回到它的起始点,即如果存在一些 t 0 >; 0 {displaystyle t_{0}>0} 使得 x ( t + t 0 ) = x ( t ) {displaystyle x(t+t_{0})=x(t)} 对于所有 t ∈ R {displaystyle tin mathbb {R} } 。 轨道是轨迹的图像,是 R 2 {displaystyle mathbb {R} {2}} 的子集。 封闭轨道或循环是封闭轨迹的图像。 极限环是一个环,它是一些其他轨迹的极限集。
属性
编辑根据若尔当曲线定理,每条闭合轨迹都将平面分为两个区域,即曲线的内部和外部。
给定一个极限环和在其内部接近极限环的轨迹,时间接近 + ∞ {displaystyle +infty } ,那么在极限环周围有一个邻域,使得内部的所有轨迹从 邻域逼近时间的极限环 + ∞ {displaystyle +infty } 。 相应的陈述适用于内部轨迹接近极限环的时间接近 − ∞ {displaystyle -infty } ,也适用于外部接近极限环的轨迹。
稳定、不稳定和半稳定极限环
编辑当时间趋近于无穷大时所有相邻轨迹都趋近极限环的情况,称为稳定或有吸引力的极限环(ω-极限环)。 相反,如果随着时间接近负无穷大,所有相邻轨迹都接近它,那么它是一个不稳定的极限环(α-极限环)。 如果有一个相邻的轨迹随着时间接近无穷大而螺旋进入极限环,而另一个轨迹在时间接近负无穷大时螺旋进入它,那么它是一个半稳定的极限环。 还有一些极限环既不是稳定的,也不是不稳定的,也不是半稳定的:例如,一个相邻的轨迹可能从外部接近极限环,但是极限环的内部被一族其他循环逼近(这不会 ‘ 是极限循环)。
稳定的极限环是吸引子的例子。 它们意味着自持振荡:闭合轨迹描述了系统的完美周期行为,并且来自该闭合轨迹的任何小扰动都会导致系统返回到它,使系统坚持极限循环。
寻找极限环
编辑每个闭合轨迹在其内部都包含系统的一个静止点,即点 p {displaystyle p} 其中 V ′ ( p ) = 0 {displaystyle V'(p)=0} 。 Bendixson-Dulac 定理和 Poincaré-Bendixson 定理分别预测了二维非线性动力系统的极限环的存在与否。
未决问题
编辑一般来说,寻找极限环是一个非常困难的问题。 平面内多项式微分方程的极限环数是希尔伯特第十六问题第二部分的主要研究对象。 例如,在平面上是否存在任何系统 x ′ = V ( x ) {displaystyle x’=V(x)} 是未知的,其中 V {displaystyle V} 的两个分量都是二次多项式 这两个变量,使得系统有超过 4 个极限环。
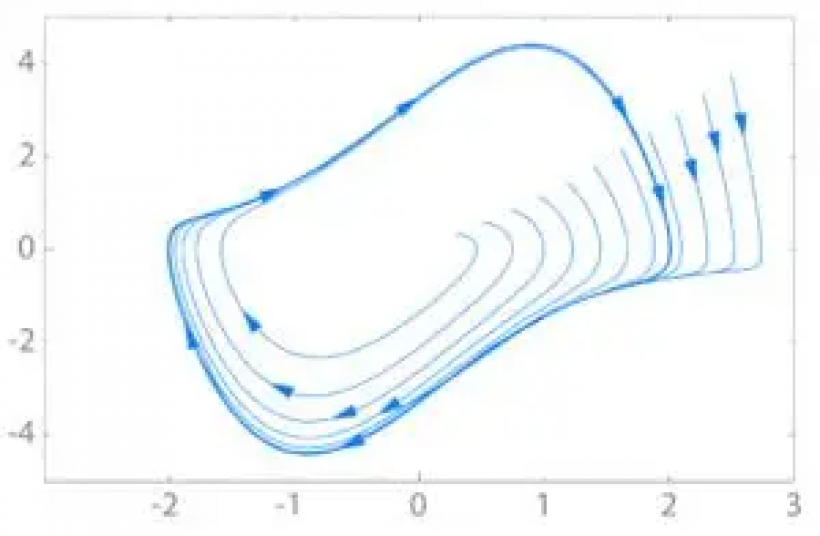
应用
编辑极限环在许多科学应用中很重要,在这些应用中,对具有自持振荡的系统进行建模。 一些例子包括:
- 空气动力学极限环振荡
- 神经元动作电位的 Hodgkin-Huxley 模型。
- 糖酵解的 Sel’kov 模型。
- 动物的基因表达、激素水平和体温的日常波动是昼夜节律的一部分,尽管这与最近的证据相矛盾。
- 癌细胞在受限微环境中的迁移遵循极限循环振荡。
- 一些非线性电路表现出极限循环振荡,这启发了最初的 Van der Pol 模型。
- 控制呼吸和造血。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/214454/
