李亚普诺夫指数

在数学中，动力系统的李亚普诺夫指数或李雅普诺夫特征指数是表征无限接近轨迹的分离率的量。 定量地，相空间中具有初始分离向量 δ Z 0 {displaystyle delta mathbf {Z} _{0}} 的两条轨迹以给定的速率发散（前提是可以在线性化近似内处理发散） 经过

| δ Z ( t ) | ≈ e λ t | δ Z 0 | {displaystyle |delta mathbf {Z} (t)|approx e{lambda t}|delta mathbf {Z} _{0}|}

其中 λ {displaystyle lambda } 是李亚普诺夫指数。

对于初始分离矢量的不同方向，分离速率可以不同。 因此，存在李亚普诺夫指数的谱——数量等于相空间的维数。 通常将最 大的一个称为最 大李亚普诺夫指数 (MLE)，因为它决定了动力系统的可预测性概念。 MLE 为正通常表示系统是混沌的（前提是满足其他一些条件，例如相空间紧凑性）。 请注意，任意初始分离向量通常包含与 MLE 相关的方向上的某些分量，并且由于指数增长率，其他指数的影响将随着时间的推移而消失。

该指数以亚历山大·李亚普诺夫 (Aleksandr Lyapunov) 的名字命名。

极限 | δ Z 0 | → 0 {displaystyle |delta mathbf {Z} _{0}|to 0} 保证了线性逼近在任何时候的有效性。

对于离散时间系统（地图或固定点迭代） x n + 1 = f ( x n ) {displaystyle x_{n+1}=f(x_{n})} ，对于以 x 0 {displaystyle x_{0}} 这转化

对于 n 维相空间中具有演化方程 x ˙ i = f i ( x ) {displaystyle {dot {x}}_{i}=f_{i}(x)} 的动力系统，谱 李亚普诺夫指数的

{ λ 1 , λ 2 , … , λ n } , {displaystyle {lambda _{1},lambda _{2},ldots ,lambda _{n}} ,,}

一般来说，取决于起点 x 0 {displaystyle x_{0}} 。 然而，我们通常会对动力系统的吸引子（或多个吸引子）感兴趣，并且通常会有一组与每个吸引子相关联的指数。 如果有多于一个，起点的选择可以决定系统结束于哪个吸引子。 （对于没有吸引子的哈密顿系统，这不是问题。）李亚普诺夫指数描述了向量在相空间的切线空间中的行为，并由雅可比矩阵定义

J i j ( t ) = d f i ( x ) d x j | x ( t ) {displaystyle J_{ij}(t)=left.{frac {df_{i}(x)}{dx_{j}}}right|_{x(t) }}

这个雅可比行列式定义了切线向量的演化，由矩阵 Y {displaystyle Y} 给出，通过方程

Y ˙ = J Y {displaystyle {dot {Y}}=JY}

初始条件 Y i j ( 0 ) = δ i j {displaystyle Y_{ij}(0)=delta _{ij}} 。 矩阵 Y {displaystyle Y} 描述了点 x ( 0 ) {displaystyle x(0)} 的微小变化如何传播到最终点 x ( t ) {displaystyle x(t)} 。

定义一个矩阵 Λ {displaystyle Lambda }（极限存在的条件由 Oseledets 定理给出）。 李亚普诺夫指数 λ i {displaystyle lambda _{i}} 由 Λ {displaystyle Lambda } 的特征值定义。

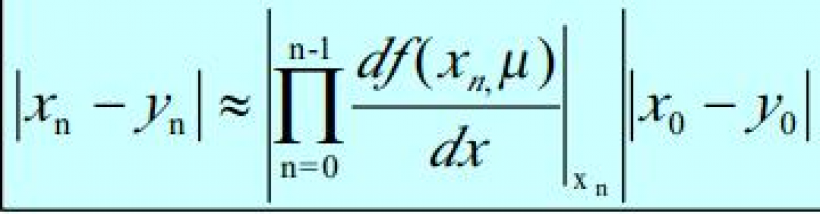
对于动力系统的遍历组件的几乎所有起点，李亚普诺夫指数集将是相同的。

为了引入李亚普诺夫指数，考虑一个基本矩阵 X ( t ) {displaystyle X(t)}（例如，对于连续系统中的平稳解 x 0 {displaystyle x_{0}} 的线性化。