李雅普诺夫稳定性

对于描述动力系统的微分方程或差分方程的解，可以讨论各种类型的稳定性。 最重要的类型是关于平衡点附近溶液的稳定性。 这可以用 Aleksandr Lyapunov 的理论来讨论。 简单来说，如果从平衡点 x e {displaystyle x_{e}} 附近开始的解永远保持在 x e {displaystyle x_{e}} 附近，那么 x e {displaystyle x_{e}} 就是 李雅普诺夫稳定。

更强烈地，如果 x e {displaystyle x_{e}} 是李雅普诺夫稳定的，并且所有在 x e {displaystyle x_{e}} 附近开始的解收敛到 x e {displaystyle x_{e}} ，那么 x e { displaystyle x_{e}} 渐近稳定。指数稳定性的概念保证了最小的衰减率，即估计解收敛的速度。

李雅普诺夫稳定性的思想可以扩展到无限维流形，称为结构稳定性，它涉及微分方程的不同但邻近的解的行为。 输入到状态稳定性 (ISS) 将 Lyapunov 概念应用于具有输入的系统。

李雅普诺夫稳定性理论不适用于保守系统，例如不表现出渐近稳定性的受限三体问题。

李雅普诺夫稳定性以亚历山大·米哈伊洛维奇·李亚普诺夫 (Aleksandr Mikhailovich Lyapunov) 的名字命名，他于 1892 年在哈尔科夫大学为论文“运动稳定性的一般问题”辩护。 通过与广泛传播的关于平衡点线性化局部方法的比较，研究非线性动力系统的稳定性。

他的作品出版，然后翻译成法文，多年来很少受到关注。 由 A. M. Lyapunov 创立的运动稳定性数学理论大 大预见了其在科学技术中的应用时间。 此外，李亚普诺夫本人并没有在这个领域进行应用，他自己的兴趣在于天文应用中旋转流体质量的稳定性。 他没有从事稳定性研究的博士生。

几十年来，稳定性理论完全被遗忘。 1930 年代数学家和机械师 Nikolay Gur'yevich Chetaev 是第 一个意识到 A. M. Lyapunov 的惊人发现的人。 N. G. Chetaev 对理论的贡献是如此重要，以至于许多数学家、物理学家和工程师都认为他是李亚普诺夫的直接继承人，并且是稳定性数学理论创建和发展的下一代科学继承人。

人们对它的兴趣突然飙升，当时发现所谓的李雅普诺夫第二方法（见下文）适用于航空航天制导系统的稳定性，该系统通常包含其他方法无法处理的强非线性。

从那时起，控制和系统文献中出现了大量出版物。最近，李雅普诺夫指数（与李雅普诺夫讨论稳定性的第 一种方法相关）的概念在与混沌理论的联系中受到了广泛关注。 李雅普诺夫平衡定性方法也被应用于寻找交通分配问题的均衡解。

考虑一个自主非线性动力系统

x ˙ = f ( x ( t ) ) , x ( 0 ) = x 0 {displaystyle {dot {x}}=f(x(t)),;;; ;x(0)=x_{0}} ,

假设 f {displaystyle f} 在 x e {displaystyle x_{e}} 处有一个平衡，所以 f ( x e ) = 0 {displaystyle f(x_{e})=0} 然后

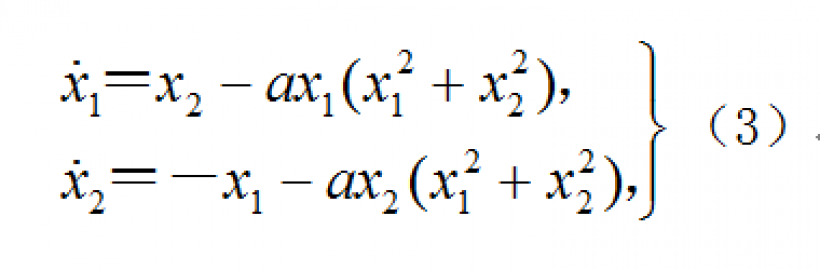
• 如果对于每个 ε > 0 {displaystyle epsilon >0} ，存在一个 δ >; 0 {displaystyle delta >0} 这样
• 如果上述系统是李雅普诺夫稳定的并且存在 δ > ; 则称上述系统的平衡是渐近稳定的。