泡利不相容原理

在量子力学中，泡利不相容原理指出两个或多个具有半整数自旋的相同粒子（即费米子）不能同时占据量子系统中的相同量子态。 该原理由奥地利物理学家沃尔夫冈·泡利 (Wolfgang Pauli) 于 1925 年针对电子制定，后来通过他 1940 年的自旋统计定理扩展到所有费米子。

对于原子中的电子，可以这样表述：一个多电子原子的两个电子不可能有四个量子数的相同值：n，主量子数； ℓ, 方位量子数; mℓ，磁量子数； 和 ms，自旋量子数。 例如，如果两个电子位于同一个轨道上，则它们的 n、ℓ 和 mℓ 值相同； 因此它们的 ms 必须不同，因此电子必须具有相反的半整数自旋投影 1/2 和 −1/2。

具有整数自旋的粒子或玻色子不受泡利不相容原理的约束：任何数量的相同玻色子都可以占据相同的量子态，例如，激光产生的光子或玻色中的原子—— 爱因斯坦凝聚体。

更严格的说法是，关于两个相同粒子的交换，总（多粒子）波函数对于费米子是反对称的，而对于玻色子是对称的。 这意味着如果两个相同粒子的空间坐标和自旋坐标互换，则总波函数的符号对费米子会改变，而对玻色子不会改变。

如果两个费米子处于相同的状态（例如，在同一个原子中具有相同自旋的相同轨道），交换它们不会改变任何东西并且总波函数将保持不变。 总波函数既可以按照费米子的要求改变符号又可以保持不变的xxx方法是这个函数必须处处为零，这意味着状态不存在。 这个推理不适用于玻色子，因为符号不会改变。

泡利不相容原理描述了所有费米子（具有半整数自旋的粒子）的行为，而玻色子（具有整数自旋的粒子）则受制于其他原理。 费米子包括夸克、电子和中微子等基本粒子。 此外，重子如质子和中子（由三个夸克组成的亚原子粒子）和一些原子（如氦-3）是费米子，因此也被泡利不相容原理描述。 原子可以有不同的整体自旋，这决定了它们是费米子还是玻色子——例如，氦 3 的自旋为 1/2，因此是费米子，而氦 4 的自旋为 0，是玻色子。 泡利不相容原理支撑着日常物质的许多特性，从大规模稳定性到原子的化学行为。

半整数自旋意味着费米子的固有角动量值为 ℏ = h / 2 π {\displaystyle \hbar =h/2\pi }（约化普朗克常数）乘以半整数（1 /2、3/2、5/2 等）。 在量子力学理论中，费米子由反对称态描述。 相反，具有整数自旋的粒子（玻色子）具有对称波函数，并且可能共享相同的量子态。 玻色子包括光子、负责超导的库珀对以及 W 和 Z 玻色子。 费米子的名字来源于它们服从的费米-狄拉克统计分布，玻色子的名字来源于玻色-爱因斯坦分布。

在 20 世纪初，具有偶数个电子的原子和分子比具有奇数个电子的原子和分子在化学上更稳定。 例如，在吉尔伯特·N·刘易斯 (Gilbert N. Lewis) 于 1916 年发表的文章《原子与分子》(The Atom and the Molecule) 中，他的六个化学行为假设中的第三个指出，原子在任何给定的壳层中倾向于持有偶数个电子，尤其是持有八个电子 ，他假设通常对称地排列在立方体的八个角上。

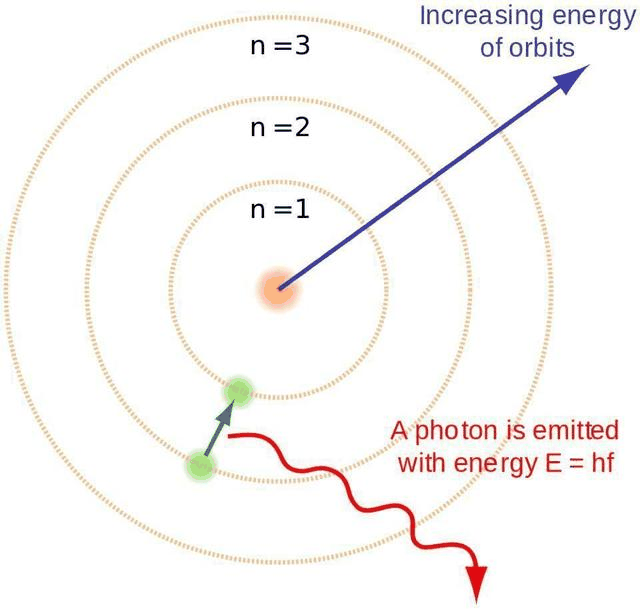
1919 年，化学家欧文·朗缪尔 (Irving Langmuir) 提出，如果原子中的电子以某种方式连接或聚集，就可以解释元素周期表。 电子群被认为占据了原子核周围的一组电子壳层。 1922 年，Niels Bohr 更新了他的原子模型，假设一定数量的电子（例如 2、8 和 18）对应于稳定的封闭壳层。

泡利寻找这些数字的解释，这些数字最初只是经验性的。 与此同时，他试图解释塞曼效应在原子光谱和铁磁性方面的实验结果。 他在 Edmund C. Stoner 1924 年的一篇论文中找到了重要线索，该论文指出，对于给定的主量子数 (n) 值，外部碱金属光谱中单个电子的能级数 所有简并能级分离的磁场等于对于相同 n 值的惰性气体封闭壳层中的电子数。