原子堆积因子
编辑在晶体学中,原子堆积因子 (APF)、堆积效率或堆积分数是晶体结构中被组成粒子占据的体积分数。 它是一个无量纲的量,总是小于单位。 在原子系统中,按照惯例,APF 是通过假设原子是刚性球体来确定的。 球体的半径被取为原子不重叠的最大值。
其中 Nparticle 是晶胞中的粒子数,Vparticle 是每个粒子的体积,Vunit cell 是晶胞所占的体积。 从数学上可以证明,对于单组分结构,最密集的原子排列的 APF 约为 0.74(见开普勒猜想),由密排结构获得。 对于多组分结构(例如填隙合金),APF 可以超过 0.74。
晶胞的原子堆积因子与材料科学的研究有关,它解释了材料的许多特性。 例如,具有高原子堆积系数的金属将具有更高的可加工性(延展性或延展性),类似于当石头靠得更近时道路更平坦,金属原子更容易滑过彼此。
单组分晶体结构
编辑下面列出了原子系统采用的常见球形填料及其相应的填料分数。
大多数金属采用 HCP、FCC 或 BCC 结构。
简单立方体
编辑对于简单的立方堆积,每个晶胞的原子数是一个。 晶胞的边长为 2r,其中 r 是原子的半径。
面心立方体
编辑对于面心立方晶胞,原子数为四个。 可以从立方体的顶角对角线到立方体同一侧的底角画一条线,等于 4r。
体心立方
编辑体心立方晶体结构的原始晶胞包含取自九个原子的几个分数(如果晶体中的粒子是原子):一个在立方体的每个角上,一个原子在中心。 因为八个角原子中每一个的体积都由八个相邻的单元共享,所以每个 BCC 单元包含两个原子的等效体积(一个在中心,一个在角上)。
每个角原子接触中心原子。 从立方体的一个角通过中心绘制到另一个角的线穿过 4r,其中 r 是原子的半径。 从几何学上看,对角线的长度是a√3。 因此,BCC结构每边的长度可以与原子半径相关:
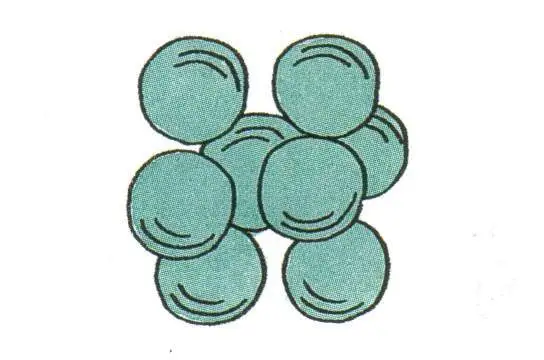
密排六方
编辑对于六方密排结构,推导类似。 这里的晶胞(相当于 3 个原始晶胞)是一个包含六个原子的六角棱柱。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/214823/
