应力强度因子

在断裂力学中，应力强度因子 (K) 用于预测由远程载荷或残余应力引起的裂纹或缺口尖端附近的应力状态（应力强度）。它是一种通常应用于均质线弹性材料的理论构造，可用于为脆性材料提供失效准则，并且是损伤容限学科中的一项关键技术。这个概念也可以应用于在裂纹尖端表现出小规模屈服的材料。

K 的大小取决于试样的几何形状、裂纹或缺口的大小和位置，以及材料上载荷的大小和分布。其中 f ( a / W ) {displaystyle f(a/W)} 是裂纹长度 a 和试样宽度 W 的试样几何相关函数，σ 是施加的应力。

线弹性理论预测裂纹尖端附近的应力分布 ( σ i j {displaystyle sigma _{ij}} ) 在极坐标 ( r , θ {displaystyle r,theta } ) 中原点为裂缝尖端

其中 K 是应力强度因子（单位为应力 × length1/2）， f i j {displaystyle f_{ij}} 是随载荷和几何形状变化的无量纲量。理论上，当 r 变为 0 时，应力 σ i j {displaystyle sigma _{ij}} 变为 ∞ {displaystyle infty } 导致应力奇异。然而，实际上，这种关系在非常靠近尖端（小 r）处失效，因为塑性通常发生在超过材料屈服强度的应力下，线性弹性解决方案不再适用。尽管如此，如果裂纹尖端塑性区与裂纹长度相比较小，则裂纹尖端附近的渐近应力分布仍然适用。

1957 年，G. Irwin 发现裂纹周围的应力可以用称为应力强度因子的比例因子来表示。他发现受到任意载荷作用的裂纹可以分解为三种线性独立的裂纹模式。如图所示，这些负载类型分为模式 I、II 或 III。模式 I 是一种开放（拉伸）模式，其中裂纹表面直接分开。模式 II 是一种滑动（面内剪切）模式，其中裂纹表面在垂直于裂纹前缘的方向上相互滑动。模式 III 是一种撕裂（反平面剪切）模式，其中裂纹表面相对于彼此移动并平行于裂纹的前缘。模式 I 是工程设计中遇到的最常见的负载类型。

不同的下标用于指定三种不同模式的应力强度因子。模式 I 的应力强度因子指定为 K I {displaystyle K_{rm {I}}} 并应用于裂纹张开模式。II 型应力强度因子 K I I {displaystyle K_{rm {II}}} 适用于裂纹滑动模式和 III 型应力强度因子 K I I I {displaystyle K_{rm {III} }} ，适用于撕裂模式。

在平面应力条件下，纯模式 I 或纯模式 II 加载下裂纹的应变能释放率 ( G {displaystyle G} ) 与应力强度因子相关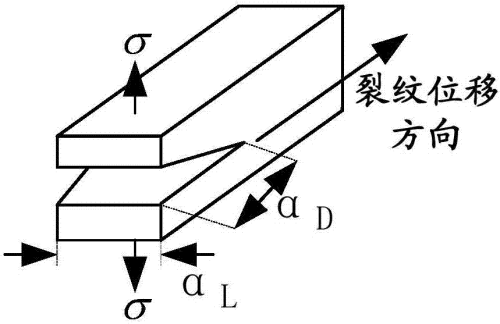

其中 E {displaystyle E} 是杨氏模量，而 ν {displaystyle nu } 是材料的泊松比。假定材料是各向同性的、均匀的和线弹性的。假定裂纹沿初始裂纹的方向延伸。