相对渗透率

在多孔介质的多相流中，相的相对渗透率是该相有效渗透率的无量纲量度。 它是该相的有效渗透率与xxx渗透率的比值。 它可以看作是达西定律对多相流的适应。

对于给定稳态条件的多孔介质中的两相流，我们可以写成

q i = − k i μ i ∇ P i for i = 1 , 2 {\displaystyle q_{i}=-{\frac {k_{i}}{\mu _{i}}}\nabla P_{ i}\qquad {\text{for}}\quad i=1,2}

其中 q i {\displaystyle q_{i}} 是通量， ∇ P i {\displaystyle \nabla P_{i}} 是压降， μ i {\displaystyle \mu _{i}} 是 粘度。 下标 i {\displaystyle i} 表示参数是针对阶段 i {\displaystyle i} 的。

k i {\displaystyle k_{i}} 这里是相磁导率（即相 i {\displaystyle i} 的有效磁导率），如通过上面的等式观察到的。

相对于渗透率，k r i {\displaystyle k_{\mathit {ri}}} ，对于阶段 i {\displaystyle i} 然后从 k i = k r i k {\displaystyle k_{i}=k_{\mathit {ri}}k} , 作为

k r i = k i / k {\displaystyle k_{\mathit {ri}}=k_{i}/k}

其中 k {\displaystyle k} 是多孔介质在单相流中的渗透率，即xxx渗透率。 相对渗透率必须介于零和一之间。

在应用中，相对渗透率通常表示为水饱和度的函数； 然而，由于毛细管滞后现象，人们通常求助于在排水下测量的函数或曲线，以及在吸水下测量的另一个函数或曲线。

在这种方法下，每一相的流动都被其他相的存在所抑制。 因此，所有相的相对渗透率之和小于 1。但是，由于达西方法忽略了相间动量传递产生的粘性耦合效应，因此获得了大于 1 的表观相对渗透率（参见下面的假设）。 这种耦合可以增强流动而不是抑制流动。 当气相以气泡或斑块（不连续）的形式流动时，已经在稠油油藏中观察到这一点。

达西定律的上述形式有时也称为达西扩展定律，用于均匀和各向同性多孔介质中的水平、一维、不混溶多相流。 流体之间的相互作用被忽略，因此该模型假设固体多孔介质和其他流体形成一个新的多孔基质，相可以通过该基质流动，这意味着流体-流体界面在稳态流动中保持静止，即 不正确，但这种近似已被证明是有用的。

每个相饱和度必须大于束缚饱和度，并且假定每个相在多孔介质中是连续的。

根据来自特殊岩心分析实验室 (SCAL) 实验的数据，可以构建相对渗透率作为饱和度（例如水饱和度）函数的简化模型。 本文将重点介绍油水系统。

水饱和度 S w {\displaystyle S_{\mathit {w}}} 是充满水的孔隙体积分数，与含油饱和度 S o {\displaystyle S_{\mathit {o}}} 类似 . 因此，饱和度本身就是缩放的属性或变量。 这给出了约束

S w + S o = 1 ⇔ S w = 1 − S o {\displaystyle S_{\mathit {w}}+S_{\mathit {o}}=1\Leftrightarrow S_{\mathit {w }}=1-S_{\mathit {o}}}

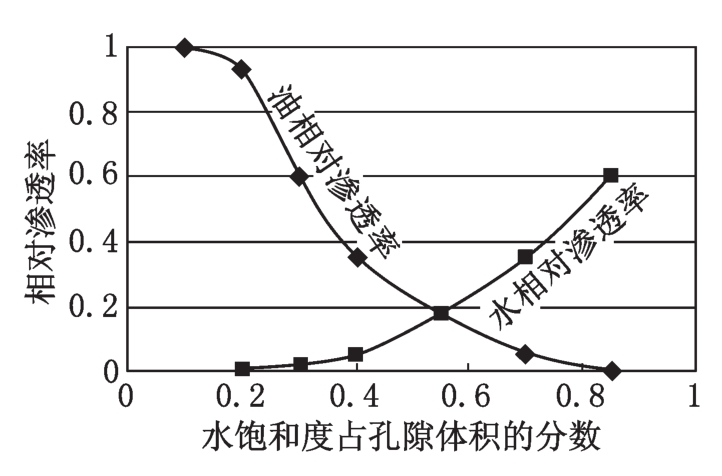
因此，油水系统中相对渗透率的模型函数或相关性通常只写为水饱和度的函数，这使得在图形表示中选择水饱和度作为水平轴很自然。 让 S w i r {\displaystyle S_{\mathit {wir}}}（也表示为 S w c {\displaystyle S_{\mathit {wc}}} 有时 S w r {\displaystyle S_{\mathit { wr}}} ) 是束缚（或最小或固有）水饱和度，并令 S o r w {\displaystyle S_{\mathit {orw}}} 是水驱（渗吸）后的残余（最小）含油饱和度。