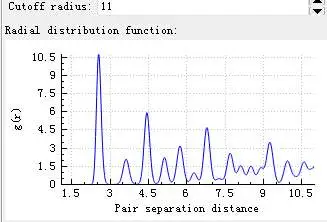
径向分布函数

在统计力学中，粒子系统（原子、分子、胶体等）中的径向分布函数（或对相关函数） g ( r ) {\displaystyle g(r)} 描述了密度如何随着 与参考粒子距离的函数。

如果给定粒子位于原点 O，并且 ρ = N / V {\displaystyle \rho =N/V} 是粒子的平均数密度，那么在一定距离处的局部时间平均密度 来自 O 的 r {\displaystyle r} 是 ρ g ( r ) {\displaystyle \rho g(r)} 。 这个简化的定义适用于均匀和各向同性的系统。 下面将考虑更一般的情况。

用最简单的术语来说，它是衡量相对于理想气体而言，在距给定参考粒子 r {\displaystyle r} 距离处找到粒子的概率。 一般算法涉及确定有多少粒子在 r {\displaystyle r} 和 r + d r {\displaystyle r+dr} 距离内。 这个一般主题描绘在右边，其中红色粒子是我们的参考粒子，蓝色粒子是那些中心在圆形壳内的粒子，以橙色点缀。

径向分布函数通常通过计算所有粒子对之间的距离并将它们合并成直方图来确定。 然后将直方图相对于理想气体归一化，其中粒子直方图完全不相关。 对于三个维度，这种归一化是系统的数密度 ( ρ ) {\displaystyle (\rho )} 乘以球壳的体积，它可以象征性地表示为 ρ 4 π r 2 d r {\ 显示样式 \rho \,4\pi r{2}dr} 。

给定势能函数，径向分布函数可以通过计算机模拟方法（如蒙特卡罗方法）或通过 Ornstein-Zernike 方程计算，使用近似闭合关系（如 Percus-Yevick 近似或超网链理论）。 它也可以通过实验确定，通过辐射散射技术或通过传统或共聚焦显微镜对足够大（微米大小）的粒子进行直接可视化。

径向分布函数非常重要，因为它可以使用 Kirkwood–Buff 解理论，将微观细节与宏观特性联系起来。 此外，通过Kirkwood-Buff理论的逆推，可以从宏观性质获得径向分布函数的微观细节。

考虑一个由 N {\displaystyle N} 粒子组成的系统，体积为 V {\displaystyle V}（对于平均数密度 ρ = N / V {\displaystyle \rho =N/V} ）和温度 T {\displaystyle T} （让我们也定义 β = 1 k T {\displaystyle \textstyle \beta ={\frac {1}{kT}}} ）。 粒子坐标为 r i {\displaystyle \mathbf {r} _{i}} ，其中 i = 1 , … , N {\displaystyle \textstyle i=1,\,\ldots ,\, N}。 粒子间相互作用产生的势能为 U N ( r 1 … , r N ) {\displaystyle \textstyle U_{N}(\mathbf {r} _{1}\,\ldots ,\ ,\mathbf {r} _{N})} 并且我们不考虑外加场的情况。

在规范系综 ( N , V , T ) {\displaystyle (N,V,T)} 中取适当的平均值，其中 Z N = ∫ ⋯ ∫ e − β U N d r 1 ⋯ d r N {\displaystyle \ textstyle Z_{N}=\int \cdots \int \mathrm {e} {-\beta U_{N}}\mathrm {d} \mathbf {r} _{1}\cdots \mathrm {d} \mathbf {r} _{N}} 构形积分，接管了粒子位置的所有可能组合。 基本配置的概率，即在 d r 1 {\displaystyle \textstyle \mathrm {d} \mathbf {r} _{1}} 中找到粒子 1，在 d r 2 {\displaystyle \ textstyle \mathrm {d} \mathbf {r} _{2}} 等由下式给出

(1)

粒子总数巨大，以至于 P ( N ) {\displaystyle P{(N)}} 本身不是很有用。 然而，也可以获得简化配置的概率，其中只有 n < 1 的位置。 N {\displaystyle n<N} 个粒子是固定的，在 r 1 … , r n {\displaystyle \textstyle \mathbf {r} _{1}\,\ldots ,\,\mathbf { r} _{n}} ，对剩余的 N − n {\displaystyle N-n} 粒子没有限制。 为此，必须在剩余坐标 r n + 1 … , r N {\displaystyle \mathbf {r} _{n+1}\,\ldots ,\,\ mathbf {r} _{N}} ：

P ( n ) ( r 1 , … , r n ) = 1 Z N ∫ ⋯ ∫ e − β U N d 3 r n + 1 ⋯ d 3 r N {\displaystyle P{(n)}(\mathbf {r} _ {1},\ldots ,\mathbf {r} _{n})={\frac {1}{Z_{N}}}\int \cdots \int \mathrm {e} { -\beta U_{N}}\,\mathrm {d} {3}\mathbf {r} _{n+1}\cdots \mathrm {d} {3}\mathbf {r } _{N}\,} 。

如果粒子是非相互作用的，在每个粒子的势能不依赖于任何其他粒子的意义上，U N ( r 1 , … , r N ) = ∑ i = 1 N U 1 ( r i ) { textstyle U_{N}(\mathbf {r} _{1},\点