碰撞理论

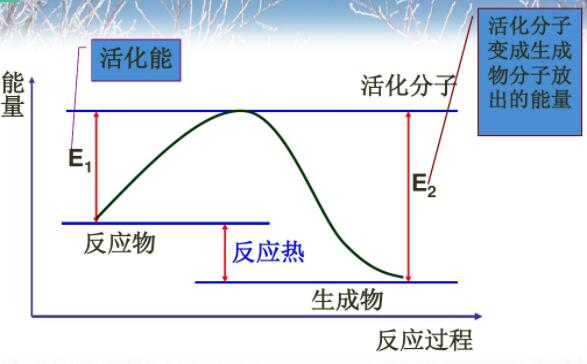
碰撞理论是用于预测化学反应速率的化学原理。 它指出，当合适的反应物粒子以正确的方向相互碰撞时，只有一定数量的碰撞会导致可察觉或显着的变化； 这些成功的变化被称为成功的碰撞。 成功的碰撞必须在撞击时刻有足够的能量，也称为活化能，以打破预先存在的键并形成所有新键。 这导致反应的产物。 增加反应物的浓度会导致更多的碰撞，从而导致更成功的碰撞。 升高温度会增加溶液中分子的平均动能，从而增加具有足够能量的碰撞次数。

当催化剂参与反应物分子之间的碰撞时，发生化学变化所需的能量较少，因此更多的碰撞具有足够的能量来发生反应。 因此反应速率增加。

碰撞理论与化学动力学密切相关。

碰撞理论预测的双分子气相反应 A + B → 产物的速率为

r ( T ) = k n A n B = Z ρ exp ⁡ ( − E a R T ) {displaystyle r(T)=kn_{text{A}}n_{text{B}}=Z rho exp left({frac {-E_{text{a}}}{RT}}right)}

在哪里：

• k 是以（分子数）−1⋅s−1⋅m3 为单位的速率常数。
• nA 是气体中 A 的数密度，单位为 m−3。
• nB 是气体中 B 的数密度，单位为 m−3。 例如。 对于气体 A 浓度为 0.1 mol⋅L−1 和 B 浓度为 0.2 mol⋅L−1 的气体混合物，A 的密度数为 0.1×6.02×1023÷10−3 = 6.02×1025 m−3，则数 B的密度为0.2×6.02×1023÷10−3 = 1.2×1026 m−3。
• Z 是以 m−3⋅s−1 为单位的碰撞频率。
• ρ {displaystyle rho } 是位阻因子。
• Ea 是反应的活化能，单位为 J⋅mol−1。
• T 是以 K 为单位的温度。
• R 是以 J mol−1K−1 为单位的气体常数。

r(T)的单位除以(1000×NA)后可换算为mol⋅L−1⋅s−1，其中NA为阿伏加德罗常数。

对于 A 和 B 之间的反应，用硬球模型计算的碰撞频率为：

Z = n A n B σ AB 8 k B T π μ AB = 10 6 N A 2 [A][B] σ AB 8 k B T π μ AB {displaystyle Z=n_{text{A}}n_{ text{B}}sigma _{text{AB}}{sqrt {frac {8k_{text{B}}T}{pi mu _{ text{AB}}}}}=10{6}N_{A}{2}{text{[A][B]}}sigma _{text{AB}}{sqrt { frac {8k_{text{B}}T}{pi mu _{text{AB}}}}}}

在哪里：

• σAB 是反应截面（单位m2），两个分子碰撞时的面积，简化为σ AB = π ( r A + r B ) 2 {displaystyle sigma _{text {AB}}=pi (r_{text{A}}+r_{text{B}}){2}} ，其中 rA 是 A 的半径，rB 是 B 的半径，单位为 m。
• kB 是玻尔兹曼常数单位 J⋅K−1。
• T为xxx温度（单位K）。
• μAB 是反应物 A 和 B 的约化质量，μ AB = m A m B m A + m B {displaystyle mu _{text{AB}}={frac {{ m_{text{A}}}{m_{text{B}}}}{{m_{text{A}}}+{m_{text{B}}}}}} ( 单位公斤）。
• NA 是阿伏加德罗常数。
• [A] 是 A 的摩尔浓度，单位为 mol⋅L−1。
• [B] 是 B 的摩尔浓度，单位为 mol⋅L−1。

如果将与量纲有关的所有单位都转换为dm，即[A]和[B]为mol⋅dm−3，σAB为dm2，玻尔兹曼常数为dm2⋅kg⋅s−2⋅K−1，则

Z = N A σ AB 8 k B T π μ AB [ A ] [ B ] {displaystyle Z=N_{text{A}}sigma _{text{AB}}{sqrt { frac {8k_{text{B}}T}{pi mu _{text{AB}}}}}[{text{A}}][{text{B }}]}

单位 mol⋅dm−3⋅s−1。

稀释气体或液体溶液中的碰撞由扩散而不是直接碰撞调节，这可以根据菲克扩散定律计算。

对于气相或液相中的稀释溶液，当扩散控制碰撞频率时，上述方程式不适用，即两个分子之间的直接碰撞不再占主导地位。 对于任何给定的分子 A，在找到要与之反应的 B 分子之前，它必须与许多溶剂分子碰撞，比方说分子 C。

考虑双分子基本反应：

A + B → C

碰撞理论认为，如果两个粒子 A 和 B 的原子核靠近一定距离，它们就会发生碰撞。 分子 A 周围可以与接近的 B 分子碰撞的区域称为反应的横截面 (σAB)，简单来说，就是对应于半径为 ( r A B {displaystyle r_ {AB}} ) 是两个反应分子的半径之和。