斜激波

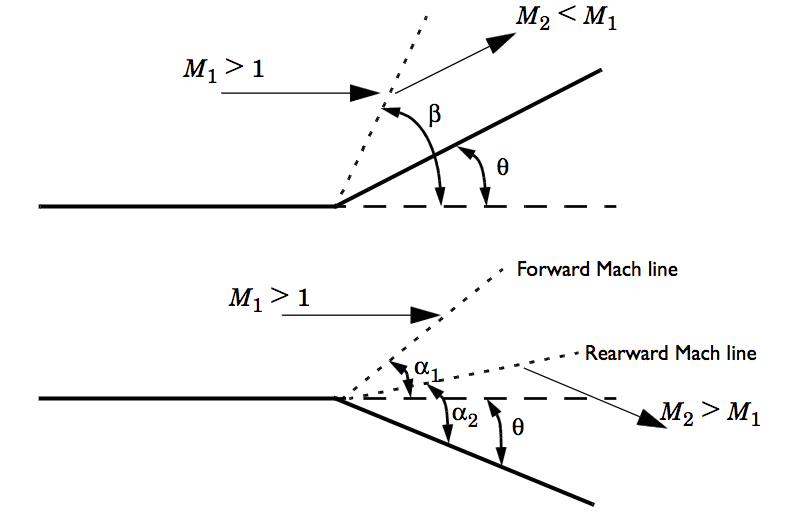
倾斜冲击波是一种冲击波，与正常冲击波不同，它相对于入射的上游流动方向倾斜。 当超音速流遇到一个有效地将流转化为自身并压缩的角时，就会发生这种情况。 激波作用后，上游流线均匀偏转。 产生倾斜冲击波的最常见方法是将楔形物放入超音速可压缩流中。 与正常冲击波类似，倾斜冲击波由一个非常薄的区域组成，气体的热力学性质在该区域发生几乎不连续的变化。 虽然上游和下游流向在正常冲击波中没有变化，但在倾斜冲击波中它们是不同的。

总是可以通过伽利略变换将斜激波转换为正激波。

对于给定的马赫数 M1 和角角 θ，可以计算出斜激波角 β 和下游马赫数 M2。 与 M2 必须始终小于 1 的正常激波不同，在斜激波中，M2 可以是超音速（弱激波）或亚声速（强激波）。 在向大气开放的流动几何结构（例如飞行器的外部）中经常观察到弱解。 在受限的几何结构中（例如在喷嘴入口内）可能会观察到强溶液。 当流量需要匹配下游高压条件时，需要强大的解决方案。 压力、密度和温度也发生不连续变化，它们都在斜激波的下游上升。

使用连续性方程和切向速度分量在激波中不发生变化的事实，三角关系最终得出 θ-β-M 方程，该方程将 θ 显示为 M1 β 和 ɣ 的函数，其中 ɣ 是热容量 比率。

在 θ-β-M 方程中，xxx角角 θMAX 存在于任何上游马赫数。 当 θ > θMAX，斜激波不再依附于角部，取而代之的是分离式弓激波。 大多数可压缩流动教科书中常见的 θ-β-M 图显示了一系列曲线，表示每个马赫数的 θMAX。 对于给定的 θ 和 M1，θ-β-M 关系将产生两个 β 角，其中较大的角度称为强冲击，较小的角度称为弱冲击。 弱激波几乎总是通过实验观察到。

与普通冲击相比，斜激波在工程应用中通常更可取。 这可以归因于这样一个事实，即与使用单个正常冲击波相比，使用一个或多个倾斜冲击波的组合会产生更有利的冲击后条件（熵增加较小，停滞压力损失较小等）。

这种技术的一个例子可以在超音速飞机发动机进气口或超音速进气口的设计中看到。 这些进气口中的一种是楔形的，可以压缩进入燃烧室的气流，同时xxx限度地减少热力学损失。 早期的超音速飞机喷气发动机进气口是使用来自单一法向冲击的压缩设计的，但这种方法将可实现的xxx马赫数限制在大约 1.6。 协和式飞机（于 1969 年首飞）使用可变几何楔形进气口实现了 2.2 马赫的xxx速度。 F-14 雄猫（F-14D 于 1994 年首次交付）采用了类似的设计，最高速度达到 2.34 马赫。

许多超音速飞机的机翼都是围绕着薄薄的菱形设计的。 以相对于超音速流线的攻角放置菱形物体将导致两个倾斜。