在相对论物理学中，双曲加速参考系的坐标构成了代表平坦闵可夫斯基时空的一部分的重要且有用的坐标图。 在狭义相对论中，一个匀速加速的粒子进行双曲线运动，为此可以选择一个它静止的匀速加速参照系作为它的适当参照系。 这种双曲线加速框架中的现象可以与均匀引力场中产生的效应进行比较。 有关平坦时空加速度的一般概述，请参阅加速度（狭义相对论）和本征参考系（平坦时空）。

本文中光速定义为c=1，惯性坐标为(X,Y,Z,T)，双曲坐标为(x,y,z,t)。 根据加速观察者的位置，这些双曲坐标可以分为两个主要变体： 如果观察者在时间 T = 0 时位于 X = 1/α 位置（其中 α 是同动加速度计测量的恒定固有加速度 ), 那么双曲坐标通常被称为润德勒坐标与相应的 Rindler 度量。 如果观察者位于时间 T = 0 的位置 X = 0，则双曲坐标有时称为 Møller 坐标或 Kottler-Møller 坐标，具有相应的 Kottler-Møller 度量。 通常与双曲线运动中的观察者相关的替代图表是使用有时称为拉斯坐标的雷达坐标获得的。 Kottler–Møller 坐标和 Lass 坐标都表示为润德勒坐标。

关于历史，这些坐标是在狭义相对论出现后不久引入的，当时它们与双曲运动的概念一起被研究（全部或部分）：阿尔伯特·爱因斯坦（AlBERT Einstein）（1907 年，1912 年）关于平坦的闵可夫斯基时空，Max Born（ 1909)、阿诺德·索末菲 (1910)、马克斯·冯·劳厄 (1911)、亨德里克·洛伦兹 (1913)、弗里德里希·科特勒 (1914)、沃尔夫冈·泡利 (1921)、卡尔·博勒特 (1922)、斯捷潘·莫霍罗维奇 (1922)、乔治·勒梅特 (1924) ), 爱因斯坦 & Nathan Rosen (1935), Christian Møller (1943, 1952), Fritz Rohrlich (1963), Harry Lass (1963), 以及 Wolfgang Rindler (1960, 1966) 的关于广义相对论的平面和弯曲时空。 有关详细信息和来源，请参阅§ 历史。

在 X {dISPlaystyle X} 方向上具有恒定固有加速度 α {diSPlaystyle alpha } 的双曲线运动物体的世界线作为固有时间

Sommerfeld 表明，可以通过将 x {displaystyle x} 定义为变量并将 α τ {displaystyle alpha tau } 定义为常量来重新解释方程，因此它表示双曲线运动中物体的同时静止形状 由同动观察者测量。 通过设置 τ = t {displaystyle tau =t} 以观察者的本征时间作为整个双曲加速坐标系的时间

微分并插入 Minkowski 度量 d s 2 = − d T 2 + d X 2 + d Y 2 + d Z 2 {displaystyle ds{2}=-dT{2}+dX{2}+dY{2} +dZ{2}} ，双曲加速框架中的度量如下

(1b)

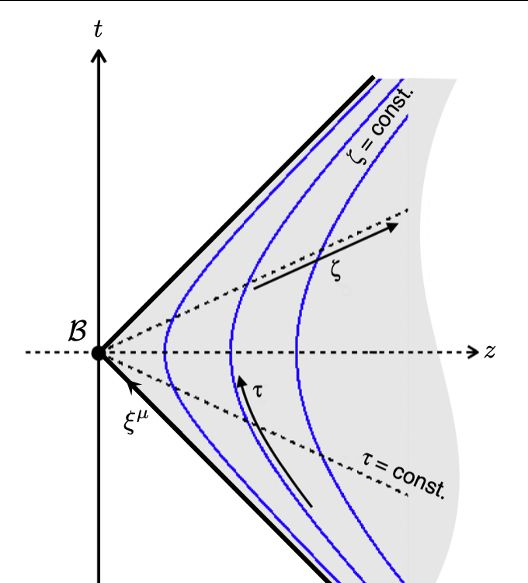
这些变换将 Rindler 观察者定义为在润德勒坐标中静止的观察者，即保持恒定的 x、y、z 并且仅随时间变化 t 。 坐标在区域 0 < 内有效。 为了维持这条世界线，观察者必须以恒定的固有加速度加速，而靠近 x = 0 {displaystyle x=0}（林德勒视界）的 Rindler 观察者具有更大的固有加速度。