稳定流形

在数学，尤其是动力系统的研究中，稳定和不稳定集合或稳定和不稳定流形的概念为吸引子或排斥器概念中体现的一般概念提供了正式的数学定义。 在双曲动力学的情况下，相应的概念是双曲集的概念。

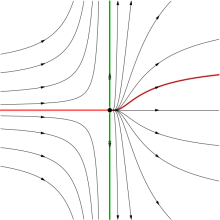
作用在土星环上的引力潮汐力提供了一个易于形象化的物理示例。 潮汐力将圆环压扁至赤道平面，即使它们在径向方向上拉伸它也是如此。 将环想象成围绕土星运行的沙子或砾石颗粒（尘埃），潮汐力是这样的，任何将颗粒推到赤道平面上方或下方的扰动都会导致该颗粒感受到恢复力，将其推回平面。 粒子有效地在谐波井中振荡，并因碰撞而衰减。 稳定方向垂直于环。 不稳定的方向是沿着任何半径，力会拉伸并将粒子拉开。 在相空间中彼此非常接近的两个粒子将受到径向力，导致它们径向发散。 这些力的李雅普诺夫指数为正； 轨迹位于双曲流形上，粒子的运动本质上是混乱的，在环中游荡。 中心歧管与环相切，粒子既不压缩也不拉伸。 这使得二阶引力占主导地位，因此粒子可以被环中的卫星或小卫星夹带，与它们锁相。 卫星的引力有效地提供了一个有规律重复的小踢，每次绕轨道运行，类似于被踢的转子，例如在锁相环中发现的。

环中粒子的离散时间运动可以用庞加莱图来近似。 该映射有效地提供了系统的传输矩阵。 与矩阵的xxx特征值相关联的特征向量是 Frobenius–Perron 特征向量，它也是不变量测度，即环中粒子的实际密度。 传递矩阵的所有其他特征向量具有较小的特征值，并且对应于衰减模式。

下面提供了系统是迭代函数或具有离散时间动态的情况的定义。 类似的概念适用于时间演化由流给出的系统。

其中 d 是 X 的度量。 当 p 是一个周期点时，这个定义显然与前面的定义一致。

现在假设 X  是紧致光滑流形，f 是 C k 微分同胚，k ≥ 1 . 如果 p {\displaystyle p} 是一个双曲周期点，稳定流形定理保证。