波波夫判据
编辑在非线性控制和稳定性理论中,波波夫判据是用于确定一类非线性系统的绝对稳定性,其非线性必须满足开放扇区条件。 虽然圆准则可以应用于非线性时变系统,但波波夫判据仅适用于自治(即时不变)系统。
系统说明
编辑Popov 研究的 Lur’e 系统子类描述如下:
x ˙ = A x + b u ξ ˙ = u y = c x + d ξ
其中 x ∈ Rn, ξ,u,y 是标量,A,b,c 和 d 具有相称的维度。 非线性元件Φ: R → R 为时不变非线性,属于开扇区(0, ∞),即Φ(0) = 0且yΦ(y) > ; 0 表示所有 y 不等于 0。
请注意,Popov 研究的系统在原点处有一个极点,并且没有从输入到输出的直接传递,从 u 到 y 的传递函数由下式给出
H ( s ) = d s + c ( s I − A ) − 1 b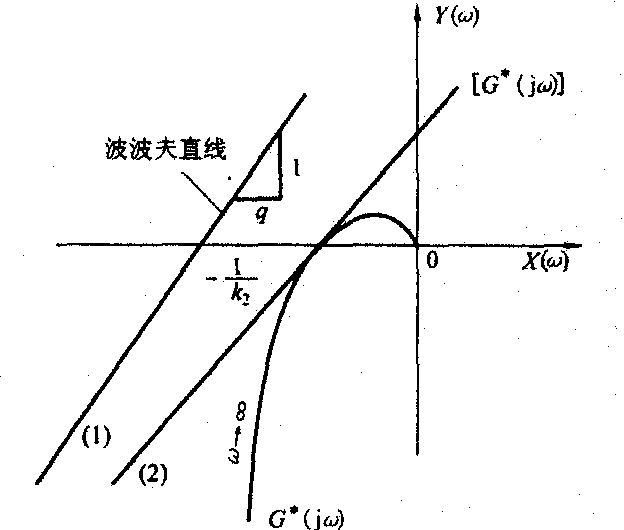
标准
编辑考虑上述系统并假设
- A 是赫尔维茨
- (A,b) 是可控的
- (A,c) 是可观察的
- d > 0 和
- Φ ∈ (0,∞)
那么如果存在数 r > 则系统是全局渐近稳定的 0 使得 inf ω ∈ R Re [ ( 1 + j ω r ) H ( j ω ) ] > 0。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/217639/
