鞍点

在数学中，鞍点或极小极大点是函数图形表面上正交方向的斜率全为零的点，但不是函数的局部极值点。 鞍点的一个示例是存在一个临界点，该临界点沿一个轴向方向具有相对最小值，而沿交叉轴具有相对xxx值。 然而，鞍点不必是这种形式。

这个名字来源于这样一个事实，即二维的原型例子是一个表面，它在一个方向上弯曲，在另一个方向上弯曲，类似于马鞍或两个山峰之间的山口，形成地形马鞍。 就等高线而言，二维中的鞍点产生等高线图，一对线相交于该点。 这种交叉点在实际军械测量地图中很少见，因为鞍点的高度不太可能与此类地图中使用的整数倍重合。 相反，鞍点显示为四组接近和远离它的等高线中间的空白区域。 对于基本鞍点，这些集合成对出现，一对相对的高对和一对相对的低对位于正交方向。 临界等高线通常不必正交相交。

检查两个实变量的实值函数 F(x,y) 的给定驻点是否为鞍点的一个简单标准是计算函数在该点的 Hessian 矩阵：如果 Hessian 是不确定的， 那么那个点就是鞍点。 例如，函数 z = x 2 − y 2在静止点 ( x , y , z ) = ( 0 , 0 , 0 ) 是矩阵

[ 2 0 0 − 2 ]

这是不确定的。 因此，该点为鞍点。 该准则仅给出了充分条件。 例如，点 ( 0 , 0 , 0 ) {\displaystyle (0,0,0)} 是函数 z = x 4 − y 4 的鞍点，但是这个函数在原点的Hessian矩阵是空矩阵，不是不定的。

用最一般的术语来说，平滑函数的鞍点是一个固定点，使得曲线/曲面/等。 在该点的邻域内并不完全位于该点切线空间的任何一侧。

在一维域中，鞍点是一个既是静止点又是拐点的点。 因为它是一个拐点，所以它不是局部极值。

鞍形曲面是包含一个或多个鞍点的光滑曲面。

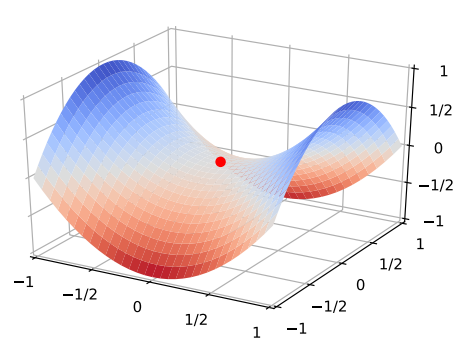
欧几里得空间中二维鞍形曲面的经典示例是二阶曲面，双曲抛物面 z = x 2 − y 2 和一张双曲面。 品客薯片或薯片是双曲抛物面形状的日常示例。

鞍形曲面具有负高斯曲率，这将它们与具有正高斯曲率的凸/椭圆曲面区分开来。 经典的三阶鞍曲面是猴鞍。

在定义在连续空间上的两人零和博弈中，平衡点是鞍点。

对于二阶线性自治系统，如果特征方程具有一正一负实特征值，则临界点为鞍点。

在受等式约束的优化中，一阶条件描述了拉格朗日量的鞍点。

在动力系统中，如果动力由可微映射 f 给出，则当且仅当 ƒ n 的微分在计算时在单位圆上没有特征值时，点是双曲线的 在这一点上。 Thena 鞍点是一个双曲周期点，其稳定流形和不稳定流形的维数都不为零。

矩阵的鞍点是一个元素，它既是其列中的xxx元素，又是其行中的最小元素。