费马原理

费马原理，也称为最短时间原理，是射线光学和波动光学之间的联系。 在其原始的强形式中，费马原理指出一条射线在两个给定点之间所走的路径是可以在最短时间内行进的路径。 为了在所有情况下都是正确的，必须通过用相对于路径变化静止的时间替换最少时间来削弱该陈述——这样路径中的偏差至多导致二阶变化 在穿越的时候。 粗略地说，一条射线路径被可以在非常接近的时间内穿过的紧密路径所包围。 可以证明，该技术定义对应于更直观的射线概念，例如视线或窄光束的路径。

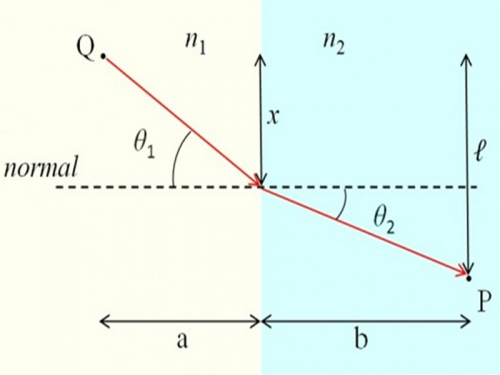
费马原理最初由法国数学家皮埃尔·德·费马于 1662 年提出，作为解释光的普通折射定律的一种方法（图 1），最初颇受争议，因为它似乎将知识和意图归于自然。 直到 19 世纪，人们才明白大自然测试替代路径的能力仅仅是波浪的基本属性。 如果给定点 A 和 B，则从 A 扩展的波阵面将扫过从 A 辐射的所有可能的光线路径，无论它们是否通过 B。 如果波前到达 B 点，它不仅会扫过从 A 到 B 的光线路径，还会扫过无数具有相同端点的附近路径。 费马原理描述了恰好到达点 B 的任何光线； 没有暗示光线知道最快的路径或打算采用该路径。

为了比较遍历时间，从一个点到下一个指定点的时间被认为是xxx个点是一个点源。 没有这个条件，遍历时间就会不明确； 例如，如果从包含 P 的任意波前 W 计算从 P 到 P' 的传播时间（图 2），则可以通过适当调整波前的角度来使该时间任意小。

将路径上的一点作为源是惠更斯原理的最低要求，也是费马原理解释的一部分。 但也可以证明，惠更斯试图应用他自己的原理（与原理本身不同）的几何构造只是对费马原理的援引。 因此，惠更斯从该构造中得出的所有结论——包括但不限于光的直线传播定律、普通反射、普通折射和冰岛水晶（方解石）的异常折射——也是费马原理的结果。

让我们假设：

• 扰动通过介质（真空或某些材料，不一定是均匀的或各向同性的）按顺序传播，没有远距离的作用；
• 在传播过程中，任何中间点 P 处的扰动对周围点的影响具有非零角扩展（就好像 P 是一个源），因此源自任何点 A 的扰动会到达任何其他点 B 通过无数条路径，B 接收到 A 处扰动的无数个延迟版本； 和
• 如果这些延迟版本的干扰在一定公差范围内同步，它们将在 B 处相互加强。

然后，如果它们的遍历时间在所述公差范围内，则从 A 到 B 的各种传播路径将相互帮助。 对于小公差（在极限情况下），如果路径是这样的，则路径的允许变化范围xxx，即其遍历时间相对于变化是固定的，因此路径的变化最多导致一秒 - 遍历时间的顺序变化。

遍历时间的平稳性最明显的例子是（局部或全局）最小值——即时间最少的路径，如费马原理的强形式。 但这个条件对论证来说并不是必不可少的。

确定了固定遍历时间的路径由相邻路径的xxx宽度走廊加强后，我们仍然需要解释这种加强如何与射线的直观概念相对应。 但是，为了解释的简洁，让我们首先将射线路径定义为静止遍历时间的路径。

如果增强从 A 到 B 的射线路径的路径走廊被严重阻塞，这将显着改变从 A 到达 B 的干扰——不像任何此类走廊外的类似大小的障碍物，阻塞不相互增强的路径。 前者的阻碍会严重干扰从 A 到达 B 的信号，而后者则不会； 因此，射线路径标志着信号路径。 如果信号是可见光，前者的障碍将显着影响在 B 处的观察者所看到的物体在 A 处的外观，而后者则不会； 所以光线路径标志着一条视线。