体积 (热力学)

系统属性注意：共轭变量以斜体显示

材料特性

• 属性数据库

可压缩性 β = − {displaystyle beta =-}
热膨胀 α = {displaystyle alpha =}

方程式

• 卡诺定理
• 克劳修斯定理
• 基本关系
• 理想气体定律

• 麦克斯韦关系
• Onsager 互惠关系
• 布里奇曼方程
• 热力学方程表

在热力学中，系统的体积是描述其热力学状态的重要广义参数。 比容是一种强度属性，是系统每单位质量的体积。 体积是状态的函数，并且与压力和温度等其他热力学性质相互依赖。 例如，根据理想气体定律，体积与理想气体的压力和温度有关。

系统的物理体积可能与用于分析系统的控制体积一致，也可能不一致。

热力学系统的体积通常是指工作流体的体积，例如活塞内的流体。 可以通过应用工作对本卷进行更改，也可以将其用于制作工作。 然而，等容过程在恒定体积下运行，因此无法产生功。 许多其他热力学过程会导致体积变化。 特别是，多变过程会导致系统发生变化，因此数量 p V n {displaystyle pV{n}} 是常数（其中 p {displaystyle p} 是压力，V {displaystyle V} 是 体积，n {displaystyle n} 是多变指数，一个常数）。 请注意，对于特定的多变指数，多变过程将等同于常数过程。 例如，对于非常大的 n {displaystyle n} 值接近无穷大，该过程变为恒定体积。

气体是可压缩的，因此它们的体积（和比容）可能会在热力学过程中发生变化。 然而，液体几乎是不可压缩的，因此它们的体积通常可以视为常数。 通常，可压缩性定义为流体或固体响应压力的相对体积变化，并且可以针对任何相的物质确定。 类似地，热膨胀是物质响应温度变化而发生体积变化的趋势。

许多热力学循环由不同的过程组成，有些过程保持恒定体积，有些则不然。 例如，蒸汽压缩制冷循环遵循制冷剂流体在物质的液态和气态之间转变的顺序。

体积的典型单位是 m 3 {displaystyle mathrm {m{3}} }（立方米）、l {displaystyle mathrm {l} }（升）和 f t 3 {displaystyle mathrm {ft} {3}}（立方英尺）。

对工作流体进行的机械功会导致系统的机械约束发生变化； 换句话说，要发生功，必须改变体积。 因此，体积是表征许多涉及功形式的能量交换的热力学过程的重要参数。

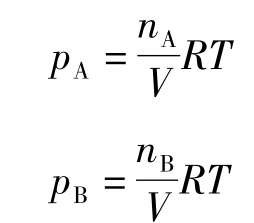
体积是一对共轭变量中的一个，另一个是压力。 与所有共轭对一样，乘积是一种能量形式。 乘积 p V {displaystyle pV} 是系统因机械功而损失的能量。 该乘积是构成焓 H {displaystyle H} 的一项：

H = U + p V , {displaystyle H=U+pV,,}

其中 U {displaystyle U} 是系统的内能。

热力学第二定律描述了对可以从热力学中提取的有用功的数量的限制