泊松括号
编辑在数学和经典力学中,泊松抽号是哈密顿力学中一个重要的二元运算,在控制哈密顿动力系统时间演化的哈密顿运动方程中起着核心作用。 泊松抽号还区分了一类坐标变换,称为正则变换,它将正则坐标系映射到正则坐标系。 正则坐标系由满足正则泊松抽号关系的正则位置和动量变量组成(下面分别用 q i {dISPlaystyle q_{i}} 和 p i {diSPlaystyle p_{i}} 表示)。 可能的规范转换集总是非常丰富。
在更一般的意义上,泊松抽号用于定义泊松代数,泊松流形上的函数代数是泊松代数的特例。 还有其他一般性的例子:它出现在李代数理论中,其中李代数的张量代数形成泊松代数; 在通用包络代数文章中给出了关于这是如何发生的详细构造。 通用包络代数的量子变形导致了量子群的概念。
属性
编辑给定两个依赖于相空间和时间的函数 f 和 g,它们的泊松抽号 { f , g } {displaystyle {f,g}} 是另一个依赖于相空间和时间的函数。
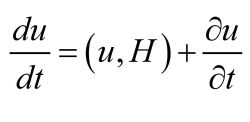
因此,辛流形上函数 f {displaystyle f} 的时间演化可以作为一个单参数辛同胚族(即规范变换)。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/221304/
