什么是函数逼近
编辑通常,函数逼近问题要求我们从定义明确的类中选择一个函数,该类以特定于任务的方式与目标函数紧密匹配(“近似”)。对于需要功能近似出现在许多分支的应用数学和计算机科学。
两大类函数逼近
编辑首先,对于已知目标函数,逼近理论是数值分析的一个分支,它研究某些已知函数(例如,特殊函数)如何可以被通常具有理想属性的特定类函数(例如,多项式或有理函数)逼近。(廉价的计算、连续性、积分和极限值等)。
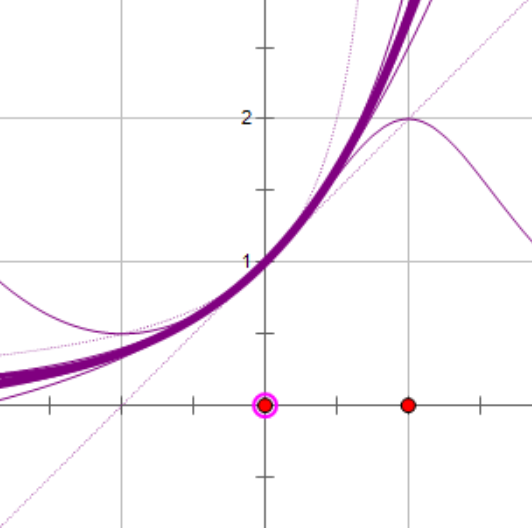
其次,目标函数,称为g,可能未知;仅提供一组形式为(x,g(x))的点,而不是明确的公式。取决于结构域和值域的克,用于逼近的几种技术克可能是适用的。例如,如果g是对实数的运算,则可以使用插值、外推、回归分析和曲线拟合技术。如果codomain(范围或目标集)的g是一个有限集,一个是处理分类问题。
在某种程度上,不同的问题(回归、分类、适应度逼近)在统计学习理论中得到了统一的处理,在那里它们被视为监督学习问题。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/124699/
