量子算法

在量子计算中，量子算法是一种在现实的量子计算模型上运行的算法，最常用的模型是计算的量子电路模型。经典（或非量子）算法是一个有限的指令序列，或解决一个问题的分步程序，其中每个步骤或指令都可以在经典计算机上执行。同样，量子算法是一个分步骤的程序，其中每个步骤都可以在量子计算机上执行。尽管所有的经典算法也可以在量子计算机上执行，但量子算法这一术语通常用于那些似乎是固有的量子算法，或使用量子计算的一些基本特征，如量子叠加或量子纠缠的算法。使用经典计算机无法解决的问题，使用量子计算机仍然无法解决。量子算法的有趣之处在于，它们可能比经典算法更快地解决一些问题，因为量子算法所利用的量子叠加和量子纠缠可能无法在经典计算机上有效地模拟。最著名的算法是Shor的因式分解算法和Grover的搜索非结构化数据库或无序列表的算法。Shor的算法比最著名的古典因式分解算法，即一般数域筛的运行速度快得多。Grover的算法比同一任务的最佳经典算法--线性搜索--的运行速度快四倍。

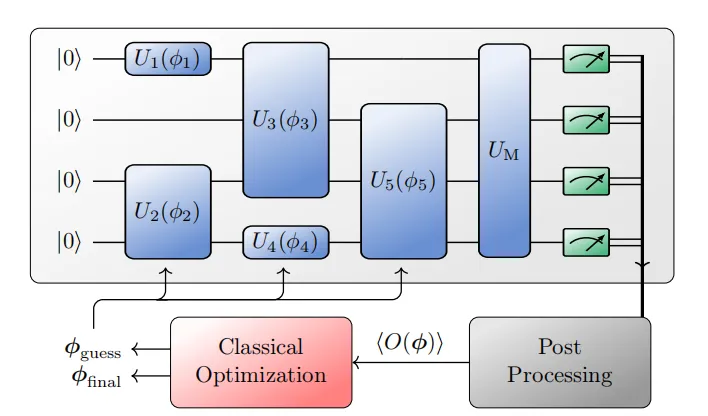
在常用的量子计算的电路模型中，量子算法通常由一个量子电路来描述，该电路作用于一些输入量子比特，并以测量结束。一个量子电路由简单的量子门组成，最多作用于固定数量的量子比特。量子比特的数量必须是固定的，因为不断变化的量子比特数量意味着非单极演化。量子算法也可以用其他的量子计算模型来表述，比如哈密尔顿神谕模型。量子算法可以按算法所使用的主要技术进行分类。量子算法中一些常用的技术/理念包括相位回授、相位估计、量子傅里叶变换、量子行走、振幅放大和拓扑量子场理论。量子算法也可以按照所解决的问题的类型进行分组，例如参见代数问题的量子算法调查。

量子傅里叶变换是离散傅里叶变换的量子类似物，在一些量子算法中被使用。哈达玛德变换也是一个量子傅里叶变换的例子，它是在场F2的n维向量空间上进行的。量子傅里叶变换可以在量子计算机上有效实现，只需使用多项式的量子门即可。如果我们同时允许有界误差的量子算法和经典算法，那么就没有加速，因为经典的概率算法可以用小概率误差的恒定数量的查询来解决这个问题。

该算法确定一个函数f是常数（在所有输入上为0或在所有输入上为1）还是平衡（对输入域的一半返回1，对另一半返回0）。伯恩斯坦-瓦兹拉尼算法伯恩斯坦-瓦兹拉尼算法是xxx个比最著名的经典算法更有效地解决一个问题的量子算法。

西蒙算法解决一个黑箱问题的速度比任何经典算法都快，包括有界误差的概率性算法。这个算法比我们认为高效的所有经典算法都实现了指数级的提速，这也是肖尔因子算法的动机。

量子相位估计算法用于确定单位门的特征向量的特征相位，给定一个与特征向量成正比的量子态并访问该门。该算法经常作为其他算法的子程序使用。

肖尔的算法在多项式时间内解决了离散对数问题和整数分解问题，而xxx的已知经典算法需要超多项式时间。这些问题不知道是在P或NP-完全的。这也是为数不多的以多项式时间解决非黑箱问题的量子算法之一，而xxx的已知经典算法运行在超多项式时间内。