量子复杂性理论

量子复杂性理论是计算复杂性理论的一个子领域，涉及使用量子计算机定义的复杂性类别，这是一种基于量子力学的计算模型。它研究计算问题的硬度与这些复杂性类的关系，以及量子复杂性类与经典（即非量子）复杂性类之间的关系。两个重要的量子复杂性类是BQP和QMA。

复杂度类是一个计算模型在某些资源约束下可以解决的计算问题的集合。例如，复杂性类P被定义为图灵机在多项式时间内可解决的问题的集合。类似地，量子复杂性类可以用计算的量子模型来定义，如量子电路模型或等价的量子图灵机。量子复杂性理论的主要目的之一是找出这些类与经典复杂性类的关系，如P、NP、BPP和PSPACE。研究量子复杂性理论的原因之一是量子计算对现代教会-图灵论的影响。简而言之，现代教会-图灵论指出，任何计算模型都可以用概率图灵机在多项式时间内进行模拟。然而，围绕教会-图灵论的问题在量子计算的背景下出现了。目前还不清楚丘吉尔-图灵论对于量子计算模型是否成立。有很多证据表明该论题不成立。概率图灵机可能不可能以多项式时间模拟量子计算模型。函数的量子计算复杂性和函数的经典计算复杂性都经常用渐近符号来表达。一些常见的函数渐近概念的形式是{displaystyleω(T(n))}表示某物在下面有界限的情况下，可以用T(n)表示。表示有东西在下面被限定为cT(n){displaystylecT(n)}表示某物被cT(n)约束在下面。

一些重要的复杂性类是P、BPP、BQP、PP和P-空间。为了定义这些，我们首先定义一个承诺问题。承诺问题是一个决策问题，它的输入被假定为从所有可能的输入字符串的集合中选择。一个承诺问题是一对{displaystyleA_{text{yes}}capA_{text{no}}==varnothing}。.前面所有的复杂度类都包含承诺问题。BQP可以由量子计算机有效解决的有界误差的问题类被称为BQP（有界误差，量子，多项式时间）。

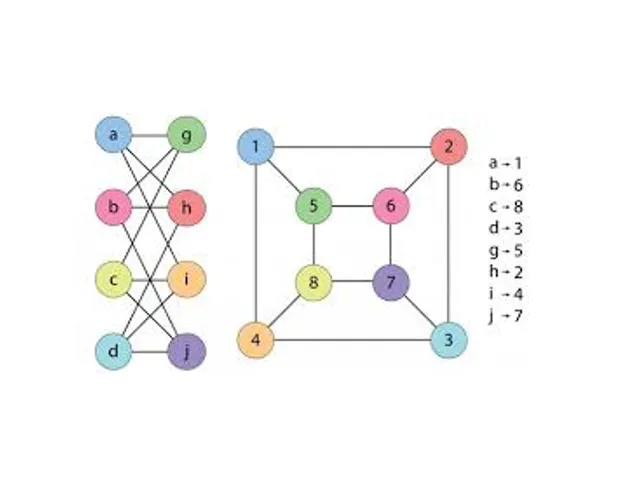
更正式地说，BQP是指错误概率最多为1/3的多项式时间量子图灵机可以解决的一类问题。作为一类概率问题，BQP是BPP（有界误差，概率，多项式时间）的量子对应物，是一类可以由有界误差的概率图灵机有效解决的问题。已知的是，这在直觉上意味着量子计算机在时间复杂性方面比经典计算机更强大。BQP是PP的一个子集。BQP与P、NP和PSPACE的确切关系尚不清楚。然而，已知的是P⊆BQP⊆PSPACE{displaystyle{mathsf{PsubseteqBQPsubseteqPSPACE}}。;也就是说，能被量子计算机有效解决的问题类别包括所有能被确定性的经典c有效解决的问题。