马尔科夫链

马尔科夫链或马尔科夫过程是一个随机模型，描述了一连串可能发生的事件，其中每个事件的概率只取决于前一个事件中达到的状态。非正式地，这可以被认为是：接下来发生的事情只取决于现在的状态。

一个可数的无限序列，其中链以离散的时间步骤移动状态，给出了一个离散时间马尔科夫链（DTMC）。一个连续时间过程被称为连续时间马尔科夫链（CTMC）。它是以数学家安德烈-马尔科夫的名字命名的。

马尔科夫链作为现实世界过程的统计模型有许多应用，如研究机动车的巡航控制系统、到达机场的顾客队列或队伍、货币汇率和动物种群动态。

马尔科夫过程是被称为马尔科夫链蒙特卡洛的一般随机模拟方法的基础，该方法用于模拟复杂概率分布的抽样，并在贝叶斯统计学、热力学、统计力学、物理学、化学、经济学、金融学、信号处理、信息理论和语音处理中找到应用。

形容词Markovian和Markov用于描述与Markov过程有关的东西。

马尔科夫过程是一个满足马尔科夫属性（有时被描述为无记忆性）的随机过程。更简单地说，它是一个可以仅根据其当前状态对未来结果进行预测的过程，最重要的是，这种预测与了解该过程全部历史的预测一样好。换句话说，以系统的当前状态为条件，其未来和过去的状态是独立的。

马尔科夫链是一种马尔科夫过程，它有一个离散的状态空间或一个离散的索引集（通常代表时间），但马尔科夫链的精确定义是不同的。例如，通常将马尔科夫链定义为具有可数状态空间的离散或连续时间的马尔科夫过程（因此不考虑时间的性质），但也通常将马尔科夫链定义为具有可数或连续状态空间的离散时间（因此不考虑状态空间）。

需要指定系统的状态空间和时间参数索引。表给出了不同级别的状态空间通用性和离散时间与连续时间的马尔科夫过程的不同实例的概述。

请注意，在文献中，对于标志着马尔可夫过程的特殊情况的一些术语的使用并没有明确的协议。通常，马尔可夫链这个术语被保留给具有离散时间集合的过程，即离散时间马尔可夫链（DTMC），但也有少数作者使用马尔可夫过程这个术语来指连续时间马尔可夫链（CTMC）而没有明确提及。

此外，还有一些被称为马尔科夫过程的其他扩展，但不一定属于这四类中的任何一类（见马尔科夫模型）。

此外，时间指数不一定是实值的；就像状态空间一样，也有可以想象的过程，用其他数学构造在指数集中移动。

请注意，一般状态空间连续时间马尔科夫链的通用程度是，它没有指定项。虽然时间参数通常是离散的，但马尔可夫链的状态空间并没有任何普遍认同的限制：该术语可以指任意状态空间上的过程。

然而，马尔可夫链的许多应用采用了有限或可数无限的状态空间，它们有更直接的统计分析。除了时间指数和状态空间参数，还有许多其他的变化、扩展和概括（见变化）。

为了简单起见，本文大部分内容集中在离散时间、离散状态空间的情况，除非另有提及。

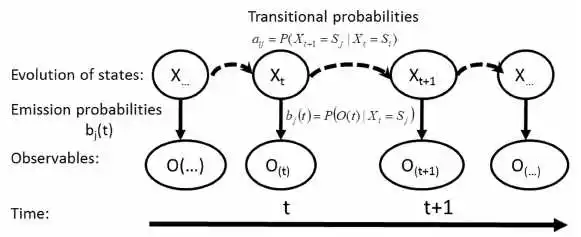
过渡系统的状态变化被称为过渡。与各种状态变化相关的概率被称为过渡概率。这个过程的特征是一个状态空间，一个描述特定过渡概率的过渡矩阵，以及一个跨越状态空间的初始状态（或初始分布）。

按照惯例，我们假设所有可能的状态和过渡都已经包括在过程的定义中，所以总是有一个下一个状态，而且过程不会终止。离散时间随机过程涉及一个系统，该系统在每一步都处于某种状态，而在每一步之间的状态是随机变化的。

这些步骤通常被认为是时间上的时刻，但它们同样可以指物理距离或任何其他离散测量。从形式上看，步骤是整数或自然数，而随机过程是这些数字的映射。