指称语义学

语言学vte在计算机科学中，指称语义学（最初被称为数学语义学或Scott-Strachey语义学）是一种通过构建描述语言表达式含义的数学对象（称为指称）来正式确定编程语言含义的方法。其他提供编程语言形式化语义的方法包括公理语义学和操作语义学。广义上讲，指称语义学关注的是寻找被称为域的数学对象，以代表程序的作用。例如，程序（或程序短语）可以通过部分函数或环境与系统之间的游戏来表示。指称语义学的一个重要原则是，语义学应该是组合式的：一个程序短语的指称应该由其子短语的指称来建立。

指称语义学起源于ChristopherStrachey和DanaScott在20世纪70年代初发表的工作。正如Strachey和Scott最初发展的那样，指称语义学将计算机程序的意义提供为一个将输入映射为输出的函数。为了赋予递归定义的程序以意义，斯科特提议在域之间使用连续函数，特别是完整的部分命令。正如下面所描述的，在研究编程语言的各个方面，如顺序性、并发性、非决定性和局部状态的适当指称语义方面的工作一直在继续。符号语义学已经为使用并发和异常等能力的现代编程语言而开发，例如，并发ML、CSP和Haskell。这些语言的语义是组合式的，即一个短语的含义取决于其子短语的含义。例如，应用性表达式f(E1,E2)的含义是根据其子句f、E1和E2的语义来定义的。在现代编程语言中，E1和E2可以被并发地评估，其中一个的执行可能会影响另一个，通过共享对象的交互导致它们的意义被定义为彼此的意义。另外，E1或E2可能会抛出一个异常，从而终止另一个的执行。下面的章节描述了这些现代编程语言的语义的特殊情况。

表征语义被赋予一个程序短语，作为从环境（持有其自由变量的当前值）到其表征的一个函数。例如，短语n*m在提供给它的两个自由变量：n和m的环境中产生了一个指称，如果在环境中n的值是3，m的值是5，那么指称就是15。一个函数可以被表示为一组有序的参数和相应的结果值对。例如，集合{(0,1),(4,3)}表示一个函数，参数0的结果为1，参数4的结果为3，否则未定义。例如，考虑一下阶乘函数，它可能被递归地定义为。

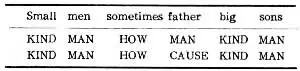
在开始时，我们从没有调用开始--因此没有任何定义。在下一个近似中，我们可以添加有序对(0,1)，因为这不需要再次调用阶乘。类似地，我们可以添加(1,1)、(2,2)等，每次连续逼近时添加一对，因为计算阶乘(n)需要调用n+1次。在极限中，我们得到一个总函数，从在其领域内的所有地方都有定义。从形式上看，我们将每个近似建模为一个部分函数然后我们可以引入符号Fn来表示F应用了n次。