简介
编辑在信号处理中,因果滤波器是一个线性和时间不变的因果系统。因果这个词表明,滤波器的输出只取决于过去和现在的输入。一个输出也取决于未来输入的滤波器是非因果的,而一个输出只取决于未来输入的滤波器是反因果的。
可实现的系统(包括过滤器)(即实时运行的系统)必须是因果的,因为这种系统不能作用于未来的输入。
实际上,这意味着最能代表时间输入的输出样本是出来的时间稍晚。数字滤波器的一个常见设计做法是通过缩短和/或时间转移非因果脉冲响应来创建一个可实现的滤波器。
如果有必要缩短,通常是通过脉冲响应与窗函数的乘积来实现的。反因果滤波器的一个例子是最大相位滤波器,它可以被定义为一个稳定的、反因果的滤波器,其倒数也是稳定的和反因果的。
因果滤波器的例子
编辑下面的定义是输入数据的移动(或滑动)平均值{dISPlaystylef(x)=int_{x-1}{x+1}s(tau),dtau=int_{-1}{+1}s(x+tau),dtau,}其中x可以代表一个空间坐标,如在图像处理中。但如果{diSPlaystyle(t)},那么这样定义的移动平均线就是非因果的(也称为非可实现的)。
那么这样定义的移动平均线就是非因果的(也叫非可实现的),因为{displaystylef(t-1)=int_{-2}{0}s(t+tau),dtau=int_{0}{+2}s(t-tau),dtau}。这是一个非实现输出的延迟版本。
任何线性滤波器(如移动平均线)都可以用一个叫做脉冲响应的函数h(t)来描述。它的输出是卷积而这两个表达式的一般相等要求h(t)=0,对于所有t<0。
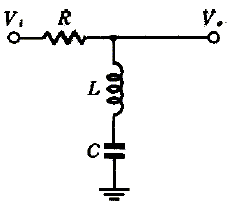
频域中因果滤波器的特征
编辑让h(t)是一个因果滤波器,有相应的傅里叶变换H(ω)。定义函数这是非因果的。另一方面,g(t)是赫米特的,因此,其傅里叶变换G(ω)是实值的。我们现在有以下关系{displaystyleh(t)=2,Theta(t)cdotg(t),}其中Θ(t)为G(ω),Θ(t)为G(ω)。其中Θ(t)是Heaviside的单位阶跃函数。
这意味着h(t)和g(t)的傅里叶变换有如下关系{displaystyle{widehat{G}}(omega),}是在希尔伯特变换中完成的。是一个在频域(而不是时域)完成的希尔伯特变换。对上述方程进行希尔伯特变换可以得到H和它的希尔伯特变换之间的这种关系。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/168704/
