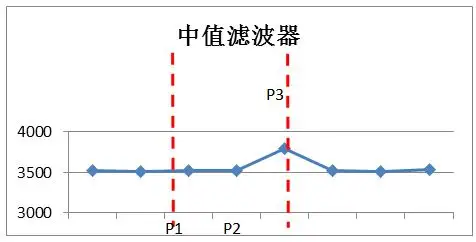
中值滤波器

中值滤波器是一种非线性数字滤波技术，通常用于去除图像或信号中的噪声。这种降噪是一个典型的预处理步骤，以改善后面的处理结果（例如，图像的边缘检测）。中值滤波在数字图像处理中应用非常广泛，因为在某些条件下，它在去除噪声的同时保留了边缘（但见下面的讨论），在信号处理中也有应用。

中位数滤波的主要思想是逐条运行信号，用相邻条目的中位数替换每个条目。邻居的模式被称为窗口，它在整个信号上逐条滑动。对于一维信号来说，最明显的窗口只是前面和后面的几个条目，而对于二维（或更高维度）数据来说，窗口必须包括给定半径或椭圆区域内的所有条目（即中位数滤波器不是一个可分离的滤波器）。

为了证明这一点，使用一个窗口大小为3，每个条目前后各有一个条目，中值滤波器将应用于以下简单的一维信号。x=(2,3,80,6,2,3).因此，中值滤波后的输出信号y将是。y1=med(2,3,80)=3,(已经有2,3,和80是递增的顺序，所以不需要排列)y2=med(3,80,6)=med(3,6,80)=6,(3,80,和6被重新排列以找到中值)y3=med(80,6,2)=med(2,6,80)=6,y4=med(6,2,3)=med(2,3,6)=3。即y=（3，6，6，3）。

在上面的例子中，由于xxx个值前面没有条目，xxx个值被重复，就像最后一个值一样，以获得足够的条目来填充窗口。这是处理信号边界缺失的窗口条目的一种方法，但还有其他的方案，这些方案具有不同的特性，在特殊情况下可能是首选。避免处理边界，无论之后是否裁剪信号或图像边界，从信号的其他地方获取条目。以图像为例，可以选择远处的水平或垂直边界的条目，缩小边界附近的窗口，使每个窗口都是满的。二维中值滤波器的伪代码一个简单的二维中值滤波器算法的代码可能是这样的。1.分配outputPixelValue[图像宽度][图像高度]2.分配window[窗口宽度×窗口高度]3.edgex:=（窗口宽度/2）向下舍入4.edgey:=（窗口高度/2）四舍五入对于x从边缘x到图像宽度-边缘x做对于y从边缘y到图像高度-边缘y做i=0对于fx从0到窗口宽度做对于fy从0到窗口高度做window[i]:=inputPixelValue[x+fx-edgex][y+fy-edgey]i:=i+1在window[]中排序条目outputPixelValue[x][y]:=window[窗口宽度*窗口高度/2］这种算法。只处理一个颜色通道，采取不处理边界的方法（见上面关于边界问题的讨论）。

算法实施问题通常，到目前为止，大部分的计算工作和时间都花在计算每个窗口的中值上。因为滤波器必须处理信号中的每一个条目，对于像图像这样的大信号，这个中值计算的效率是决定算法运行速度的关键因素。上面描述的天真实现对窗口中的每一个条目进行排序以找到中值；然而，由于只需要数字列表中的中间值，选择算法的效率可以高得多。此外，某些类型的信号（对于图像来说常常是这样）使用整数表示：在这些情况下，直方图中值的效率会高得多，因为从窗口到窗口更新直方图很简单，而且寻找直方图的中值也不是特别繁重。

中位数滤波是一种平滑技术，线性高斯滤波也是如此。所有的平滑技术都能有效地去除信号的平滑斑块或平滑区域的噪声，但对边缘有不利的影响。但通常情况下，在减少信号中的噪声的同时，保留边缘也很重要。例如，边缘对于图像的视觉外观是至关重要的。对于小到中等程度的高斯噪声，在给定的固定窗口大小下，中值滤波器在去除噪声的同时保留边缘方面明显优于高斯模糊。然而，对于高水平的噪声，它的性能并不比高斯模糊好多少，而对于斑点噪声和盐和胡椒噪声（冲动噪声），它特别有效。正因为如此，中值滤波在数字图像处理中得到了非常广泛的应用。