归纳类型

在类型理论中，如果一个系统具有从创建该类型的常量和函数中创建新类型的设施，那么它就具有归纳类型。该功能的作用类似于编程语言中的数据结构，并允许类型理论增加数字、关系和树等概念。顾名思义，归纳类型可以是自指的，但通常只允许结构性递归的方式。标准的例子是使用Peano的编码对自然数进行编码。归纳式nat:Type:=|0:nat|S:nat->nat。在这里，一个自然数是由常数0或通过将函数S应用于另一个自然数而产生的。S是继任函数，表示在一个数上加1。因此，0是0，S0是1，S（S0）是2，S（S（S0））是3，以此类推。自引入以来，归纳类型已经被扩展到编码越来越多的结构，同时仍然是预测性的并支持结构递归。

归纳类型通常带有一个函数来证明关于它们的属性。因此，nat可能带有。nat_elim:(forallP:nat->Prop,(P0)->(foralln,Pn->P(Sn))->(foralln,Pn))。这是nat类型的结构递归的预期函数。

W-类型是直觉类型理论（ITT）中的有根有据的类型。它们概括了自然数、列表、二叉树和其他树形数据类型。让U是一个类型的宇宙。给定一个类型A：U和一个依赖族B：A→U，我们可以形成一个W类型.类型A可以被认为是被定义的归纳类型的（可能是无限多的）构造函数的标签，而B表示每个构造函数的（可能是无限的）arity。W-类型（resp.M-类型）也可以被理解为井底之蛙（resp.非井底之蛙），其节点由元素a：A标记，由a标记的节点有B（a）多条子树。每个W型与一个所谓的多项式漏斗的初始代数同构。让0、1、2等为有限类型，居民为11：1、12、22：2等。我们可以把自然数定义为W型与f:2→U的定义是：f(12)=0（代表零的构造函数，不需要参数），f(22)=1（代表继承函数，需要一个参数）。

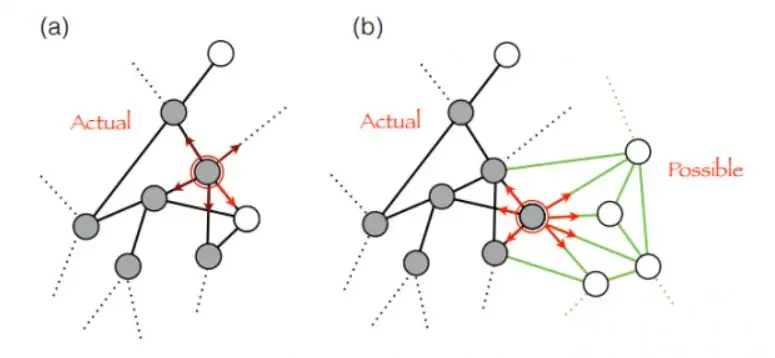
我们可以在一个类型A：U上定义列表为{displaystylef(operatorname{inr}(a))}则对应于空列表的构造函数。的值对应于将a追加到另一个列表的开头的构造函数。通用W型的元素的构造函数W-类型的消除规则与树的结构归纳法类似。如果，只要有一个属性（在命题即类型的解释下），那么对某棵树的所有子树都成立，对该树也成立，那么它对所有树都成立。在扩展类型理论中，W-类型（resp.M-类型）可以被定义为多项式漏斗的初始集合体（resp.最终集合体），直至同构。在这种情况下，初始性（res.finality）的属性直接对应于适当的归纳原则。在具有单等价公理的扩展类型理论中，这种对应关系直到同构（命题平等）才成立。M-类型是W-类型的对偶，它们代表硬币