类型（类型理论）

在被称为类型理论的数理逻辑和计算机科学领域，类型是一个类型构造器的类型，或者不那么常见的是一个高阶类型操作符的类型。一个类型系统本质上是一个简单类型的lambdacalculus，它有一个原始的类型，表示为并称为类型，它是任何不需要任何类型参数的数据类型的类型。类型有时被混乱地描述为（数据）类型的类型，但它实际上更像是一个算术指定器。在语法上，我们很自然地认为多态类型是类型构造器，因此非多态类型是空态类型构造器。但是所有的空类型构造器，也就是所有的单态类型，都有相同的、最简单的种类；即由于高阶类型操作符在编程语言中并不常见，在大多数编程实践中，种类被用来区分数据类型和用于实现参数化多态性的构造函数的类型。类型出现在语言中，无论是明确的还是隐含的，这些语言的类型系统以程序可访问的方式解释参数多态性，例如C++、Haskell和Scala。，发音为type，是所有数据类型的种类，被视为空类型构造器，在这里也被称为适当类型。这通常包括函数式编程语言中的函数类型。{displaystyle*rightarrow*}是单数类型的种类。是二元类型构造函数的种类，例如一对类型构造函数，也是函数类型构造函数的种类，不要与它的应用结果相混淆，它本身是一个函数类型，因此是种类是指从单数类型构造器到适当类型的高阶类型运算符的种类。Haskell中的种类。Haskell98的类型系统正好包括两种类型。发音的类型是所有数据类型的种类。

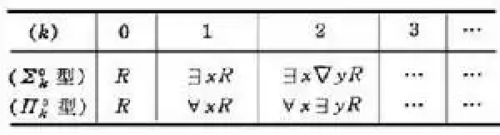
{displaystylek_{1}rightarrowk_{2}}是单数类型构造函数的种类。是一个单数类型构造函数的类型，它接收一个类型为一个居住的类型（在Haskell中称为适当的类型）是一个有值的类型。例如，忽略那些使情况复杂化的类型，4是一个Int类型的值，而[1,2,3]是一个[Int]类型的值（Ints的列表）。因此，Int和[Int]有种但任何函数类型也是如此，例如，Int->Bool或甚至Int->Int->Bool。一个类型构造函数接受一个或多个类型参数，当提供足够的参数时产生一个数据类型，也就是说，由于currying，它支持部分应用。

标准Haskell不允许多态的种类。这与类型上的参数化多态性相反，在Haskell中支持这种多态性。例如，在下面的例子中。，除非类型明确指出了其他情况。因此，类型检查器将拒绝以下对Tree的使用。GHC有一个扩展PolyKinds，它和KindSignatures一起，允许多态的类型。